Jag inser att jag inte hinner idag, måste fixa ihop en del saker till i morgonMikael_L skrev:
Det här var ju ett kul problem. Varför finns det inte redan en modell för det?
Om jag tänker rätt så är det som krävs en formel för uppvärmning av säkringen vid en given ström samt säkringens värmeförlust till omgivningen. Någonstans måste man nog anta något slags omgivningstemperatur, med något rimligt värde.
Uppvärmningen borde rimligen gå att räkna på med Ohms lag om man verkligen vill, dvs räkna effekten som en given ström värmer upp säkringen med. Det blir inte helt linjärt om man tar med i beräkningen att resistiviteten för koppar ökar med ökad temperatur men den effekten är sannolikt ganska liten.
Avkylningen blir inte linjär eftersom värmeavgivningen till omgivningen ökar med ökat delta-T.
Kan man tänka sig en modell där man i princip räknar "Ampereminuter" för uppvärmning och samtidigt beräknar avkylningen givet antal ampereminuter? Eftersom avkylningen är ickelinjär får man kanske ha en formel av modellen AM*k*t där k = 1/x med ett lämpligt x och AM är aktuellt värde "Ampereminuter"?
Excelformeln skulle då bli, rad för rad,
Aktuell ström | tid* | antal ampereminuter för denna rad | avkylning för denna rad ** | aktuellt värde ampereminuter***
* om tiden är samma mellan varje mätpunkt om man antar att strömmen är konstant över hela tiden kan man rationalisera bort detta och bara multiplicera aktuell ström med mätperiodens längd
** beräknas mot föregående rads aktuella värde
*** formeln blir då aktuellt värde ampereminuter från raden ovanför + antal ampereminuter för denna rad - avkylningseffekt
Eftersom jag är kass på excel är jag inte säker på att jag tänkt rätt överhuvudtaget men detta borde ge GK100s läckande hink, med en temperaturberoende avkylning. Vill man göra en logaritmfunktion av avkylningen kan man göra det också.
Hur ska man använda detta i praktiken då? Ja, man får bestämma sig för ett ampereminutvärde som inte får överskridas och sedan se om man gör det vid något tillfälle. Det kan enkelt göras med MAX för aktuell kolumn.
Vilket ska det värdet vara? Tja, ingen aning. Man får labba lite med vad verkliga värden skulle ge, te.x. att en säkring ska klara fem minuter med 50% överlast enligt spec i orginalposten. För en 125 A säkring är 50% överlast 187,5, så detta skulle ge 937,5 ampereminuter som ett tak på toleransen. Samtidigt vet vi att den klarar märkström (och lite till obegränsat) så 625 ampereminuter måste vara minsta "avkylningen" under de fem minuterna. Man kanske bara ska räkna på uppvärmningseffekten av överströmmen för att förenkla?
Velanders formel ser jag inte riktigt som applicerbar här eftersom vi inte behöver estimera maxförbrukning, den vet vi via mätning. Frågan är hur ofta och länge vi ligger på en given belastning och det förstår jag det inte som att den svarar på.
Om jag tänker rätt så är det som krävs en formel för uppvärmning av säkringen vid en given ström samt säkringens värmeförlust till omgivningen. Någonstans måste man nog anta något slags omgivningstemperatur, med något rimligt värde.
Uppvärmningen borde rimligen gå att räkna på med Ohms lag om man verkligen vill, dvs räkna effekten som en given ström värmer upp säkringen med. Det blir inte helt linjärt om man tar med i beräkningen att resistiviteten för koppar ökar med ökad temperatur men den effekten är sannolikt ganska liten.
Avkylningen blir inte linjär eftersom värmeavgivningen till omgivningen ökar med ökat delta-T.
Kan man tänka sig en modell där man i princip räknar "Ampereminuter" för uppvärmning och samtidigt beräknar avkylningen givet antal ampereminuter? Eftersom avkylningen är ickelinjär får man kanske ha en formel av modellen AM*k*t där k = 1/x med ett lämpligt x och AM är aktuellt värde "Ampereminuter"?
Excelformeln skulle då bli, rad för rad,
Aktuell ström | tid* | antal ampereminuter för denna rad | avkylning för denna rad ** | aktuellt värde ampereminuter***
* om tiden är samma mellan varje mätpunkt om man antar att strömmen är konstant över hela tiden kan man rationalisera bort detta och bara multiplicera aktuell ström med mätperiodens längd
** beräknas mot föregående rads aktuella värde
*** formeln blir då aktuellt värde ampereminuter från raden ovanför + antal ampereminuter för denna rad - avkylningseffekt
Eftersom jag är kass på excel är jag inte säker på att jag tänkt rätt överhuvudtaget men detta borde ge GK100s läckande hink, med en temperaturberoende avkylning. Vill man göra en logaritmfunktion av avkylningen kan man göra det också.
Hur ska man använda detta i praktiken då? Ja, man får bestämma sig för ett ampereminutvärde som inte får överskridas och sedan se om man gör det vid något tillfälle. Det kan enkelt göras med MAX för aktuell kolumn.
Vilket ska det värdet vara? Tja, ingen aning. Man får labba lite med vad verkliga värden skulle ge, te.x. att en säkring ska klara fem minuter med 50% överlast enligt spec i orginalposten. För en 125 A säkring är 50% överlast 187,5, så detta skulle ge 937,5 ampereminuter som ett tak på toleransen. Samtidigt vet vi att den klarar märkström (och lite till obegränsat) så 625 ampereminuter måste vara minsta "avkylningen" under de fem minuterna. Man kanske bara ska räkna på uppvärmningseffekten av överströmmen för att förenkla?
Velanders formel ser jag inte riktigt som applicerbar här eftersom vi inte behöver estimera maxförbrukning, den vet vi via mätning. Frågan är hur ofta och länge vi ligger på en given belastning och det förstår jag det inte som att den svarar på.
inte så säker på att du gillar mina visualiseringar, men du får en till 😉GK100 skrev:
och lite rå excel-godis...
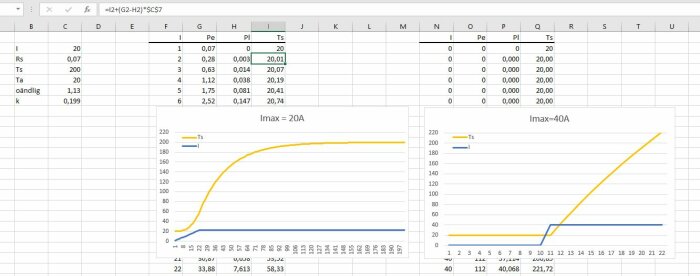
en ansats till att betrakta problemet, men har för mig tre obekanta parametrar – säkringens resistans, säkringstrådens smälttemperatur och värmeledningsförmågan, men dessa kunde jag anpassa till att efterlikna egenskaperna för en 20A säkring
ansatsen kan vara tokig, termodynamik har inte varit min profession – däremot att mäta, analysera och visualisera företeelser, skeenden och förlopp som inte enbart bygger på fysikaliska samband och som ofta aldrig tidigare någonsin studerats – människans oförutsägbara beteende som ställer saker på ända har varit ett centralt osäkerhetsmoment – där hör jag hemma
Redigerat:
Varför jag inte skulle gilla dina visualiseringar förstår jag inte de är väl alltid bra och vettiga här som i andra trådar.harka skrev:
Man behöver inte åtminstone grovt och inledningsvis bry sig om diverse av parametrarna likt de du är inne på. Räcker bra med I2t integrerat och en uppskattad termisk läcka proportionell åt andra hållet. Så du är rätt på det för att kunna gå vidare som jag ser det. Resultatet av en mätserie likt de Mikael visar bör vara en grafik över tiden som bara visar hur resultatet av ovanstående beter sig och utan anspråk på korrekta temperaturer det är först intressant att se hur och var eventuella toppar ligger.
Själv jobbar jag ganska ofta med olika mer eller mindre sofistikerade modeller använda för tex fall likt dessa men givetvis inte för en säkring eller elanläggning av typen här på BH. I ElDim trådarna sen mer än 10 år tillbaks var det uppe ibland som lite kuriosa hur man hanterar fallen som inte ses som adiabatiska dvs där tumreglerna som utmynnar i t < 5 s inte gäller typiskt för tex smältsäkringar, kortslutningsförlopp runt effektbrytare osv. Att gräva ner sig ger inte mycket här mer än att om man är intresserad kan man lära sig lite tänk fysikaliskt och hur man ofta lätt kan sätta mycket "väsentligen ett" och få en ökad intuition för när/var/hur man kan gena praktiskt.
Såhär ska det nog vara.
Och det finns fortfarande saker att fixa och snygga till.
Spännande saker ni funderar på, tommib, harka och GK100.
Jag påtar på här.
Jag känner att jag börjar ha något ganska klart, lite användbart t.o.m.
Jag ska kolla genom lite till, sen kan jag nog publicera XL-arket också.
Jag letade lite efter om det går att hitta tabellerade värden för pre-arc-tiden för säkringar,
Då stötte jag på denna, de tre sista sidorna tycker jag innehåller lite om tekniken i säkringar på nästan lekmannanivå, men väldigt bra skrivet. Jag tycker att jag lärde mig lite själv, och det djupdyker trots allt inte avgrundsdjupt i teknik och fysik ändå.
https://www.chscontrols.se/fileadmin/user_upload/product-images/PM1082.pdf
Jag råkade också på en sak som verkar vråltung - fysik och matematik på hög nivå, jag ska kolla lite till på den och se om den träffar rätt, då publicerar jag den här.
Jag tror den är förbi min nivå och mitt mål här, men några verkar ju ha nappat på tanken att djupdyka i fysiken och matematiken där.
Jag känner att jag börjar ha något ganska klart, lite användbart t.o.m.
Jag ska kolla genom lite till, sen kan jag nog publicera XL-arket också.
Jag letade lite efter om det går att hitta tabellerade värden för pre-arc-tiden för säkringar,
Då stötte jag på denna, de tre sista sidorna tycker jag innehåller lite om tekniken i säkringar på nästan lekmannanivå, men väldigt bra skrivet. Jag tycker att jag lärde mig lite själv, och det djupdyker trots allt inte avgrundsdjupt i teknik och fysik ändå.
https://www.chscontrols.se/fileadmin/user_upload/product-images/PM1082.pdf
Jag råkade också på en sak som verkar vråltung - fysik och matematik på hög nivå, jag ska kolla lite till på den och se om den träffar rätt, då publicerar jag den här.
Jag tror den är förbi min nivå och mitt mål här, men några verkar ju ha nappat på tanken att djupdyka i fysiken och matematiken där.
Sådana här time/current kurvor är lätta att hitta.
Men finns detta att finna i tabell-form?
Alltså från delar av sekund till kanske uppåt en timme?
Eller finns det matematiskt utryckt som går att använda (med någon logaritmisk funktion i, antar jag).
Men finns detta att finna i tabell-form?
Alltså från delar av sekund till kanske uppåt en timme?
Eller finns det matematiskt utryckt som går att använda (med någon logaritmisk funktion i, antar jag).
finns ju i diagrammet från 0.004 s till 8000 s
räcker inte det??
både tid och ström är log10-skala och skulle man göra en linjär tabell i tex. 1/1000-dels sekund uppdelning till att räcka till 8000 sekunder så blir den listan väldigt stor. och excel med över hundra tusen rader är inte kul att leka med då den körs enkeltrådad på datorn...
Eftersom linjerna är knäckta även i logaritmisk skala så krävs det en högre ordningens polynom för att beskriva linjen som en ekvation
du får titta på någon kurvanpassningsprogram för att få ut ekvationerna för linjerna och komma ihåg att dessa kurvor är i log10 skala både på x och y-axeln.
---
Sedan har vi det här med effektfaktorer på strömmen för olika förbrukare - och med effektfaktorer menar jag här beroende av strömmens övertonshalt av distorderad sinuskurva - inte förskjutningsström för att lasten är reaktiv.
Tex. om vi jämför en 100 Watts klassisk glödlampa med samlade effekten av all LED-belysning som också drar tillsammans 100 Watt men har effektfaktorn säg här 0.33 - vilket innebär att för samma effekt för båda så drar LED-belysningen 3 ggr mer ström och värmeutvecklingen i säkringen blir 9 ggr högre.
Till detta, ju mer pulsig ström ( i periodtopparna) förbrukaren genererar dvs. allt högre crestfaktor lasten har, ju mindre överström tål säkringen då värmeutvecklingen under strömpulsen blir hetare och blir mer koncentrerad i säkringstrådens centrum under kortare tid och mindre av dess värme hinner ut i sanden/luften under halvperioden i jämförelse med värmeutveckling som blir med en 50Hz med sinusformad ström.
Med andra ord laster med hög ström-övertonshalt kan dra ned säkringens tålighet för kraftigt distorderade överströmmar från switchade nätaggregat mfl. (tänk invertersvetsar, invertervärmepumpar etc.) gentemot de sinusformade strömmar som tex. kan genereras under en elmotorstart.
Vi hade Switchade nätaggregat för 60 Volt och 20 ampere som kunde rycka sönder 10 A tröga säkringar på ca 1 timme trots att effektuttaget ur dessa låg strax under 1200 Watt pga. deras dåliga effektfaktor mot elnätet - detta tiden innan man började med tvånget med PFC-kretsar i större nätaggregaten på 1990-talet, men problemet kvart står fortfarande om man har installationer med väldigt många mindre energisparlampor och LED-lampor med mycket simpla switcade omvandlare i sig då dessa inte har PFC-krav på sig (ännu) dvs 10 st 5W LED GU10-lampor kan dra ström för motsvarande 150-200 Watt och med de fula strömspikarna när de laddar upp sina små kondensatorer på period-topparna så kanske det motsvarar värmeutveckling > 300 Watt räknat som ström i säkringens smälttråd just för att det är väldigt mycket värme/effekt på väldigt kort tid runt halvperiodtoppen per halvperiod i jämförelse när hela effekten är spridd i som kvadrerad halvsinusperiod över hela halvperioden och hinner kylas mer under tiden värmen produceras.
räcker inte det??
både tid och ström är log10-skala och skulle man göra en linjär tabell i tex. 1/1000-dels sekund uppdelning till att räcka till 8000 sekunder så blir den listan väldigt stor. och excel med över hundra tusen rader är inte kul att leka med då den körs enkeltrådad på datorn...
Eftersom linjerna är knäckta även i logaritmisk skala så krävs det en högre ordningens polynom för att beskriva linjen som en ekvation
du får titta på någon kurvanpassningsprogram för att få ut ekvationerna för linjerna och komma ihåg att dessa kurvor är i log10 skala både på x och y-axeln.
---
Sedan har vi det här med effektfaktorer på strömmen för olika förbrukare - och med effektfaktorer menar jag här beroende av strömmens övertonshalt av distorderad sinuskurva - inte förskjutningsström för att lasten är reaktiv.
Tex. om vi jämför en 100 Watts klassisk glödlampa med samlade effekten av all LED-belysning som också drar tillsammans 100 Watt men har effektfaktorn säg här 0.33 - vilket innebär att för samma effekt för båda så drar LED-belysningen 3 ggr mer ström och värmeutvecklingen i säkringen blir 9 ggr högre.
Till detta, ju mer pulsig ström ( i periodtopparna) förbrukaren genererar dvs. allt högre crestfaktor lasten har, ju mindre överström tål säkringen då värmeutvecklingen under strömpulsen blir hetare och blir mer koncentrerad i säkringstrådens centrum under kortare tid och mindre av dess värme hinner ut i sanden/luften under halvperioden i jämförelse med värmeutveckling som blir med en 50Hz med sinusformad ström.
Med andra ord laster med hög ström-övertonshalt kan dra ned säkringens tålighet för kraftigt distorderade överströmmar från switchade nätaggregat mfl. (tänk invertersvetsar, invertervärmepumpar etc.) gentemot de sinusformade strömmar som tex. kan genereras under en elmotorstart.
Vi hade Switchade nätaggregat för 60 Volt och 20 ampere som kunde rycka sönder 10 A tröga säkringar på ca 1 timme trots att effektuttaget ur dessa låg strax under 1200 Watt pga. deras dåliga effektfaktor mot elnätet - detta tiden innan man började med tvånget med PFC-kretsar i större nätaggregaten på 1990-talet, men problemet kvart står fortfarande om man har installationer med väldigt många mindre energisparlampor och LED-lampor med mycket simpla switcade omvandlare i sig då dessa inte har PFC-krav på sig (ännu) dvs 10 st 5W LED GU10-lampor kan dra ström för motsvarande 150-200 Watt och med de fula strömspikarna när de laddar upp sina små kondensatorer på period-topparna så kanske det motsvarar värmeutveckling > 300 Watt räknat som ström i säkringens smälttråd just för att det är väldigt mycket värme/effekt på väldigt kort tid runt halvperiodtoppen per halvperiod i jämförelse när hela effekten är spridd i som kvadrerad halvsinusperiod över hela halvperioden och hinner kylas mer under tiden värmen produceras.
Redigerat:
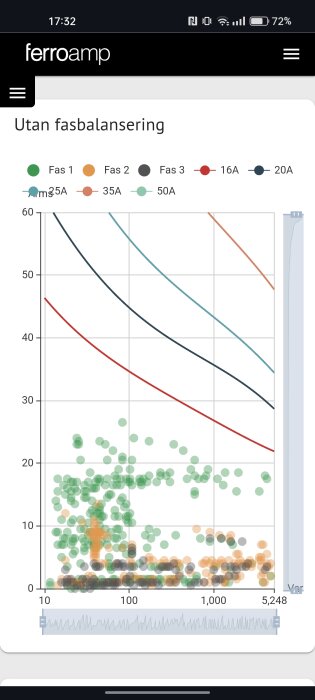
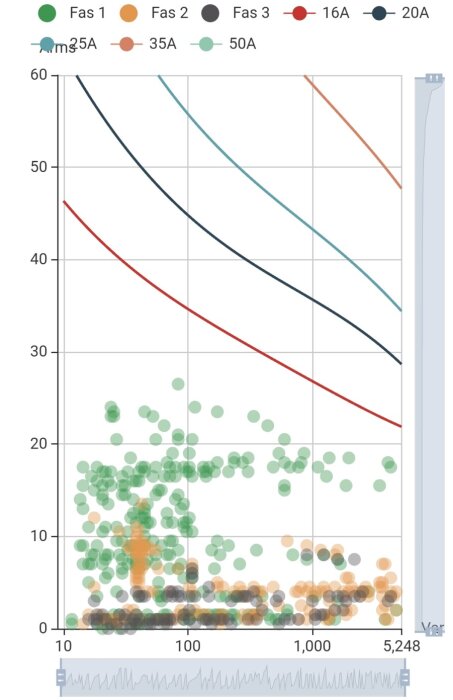
Ferroamp har ett analysverktyg för säkringsstorlek baserat på hur husets förbrukning sett ut över tid. Givetvis måste man ha en Ferroamp växelriktare/energyhub installerad men så här ser deras kurvor ut (hoppas det tillför något i tråden).
Y-axeln är ampere per fas.
X-axeln är tid i sekunder.
Linjerna representerar vilken huvudsäkring de rekommenderar, röd linje är 16A.
Plupparna är uppmätta värden per fas.
Y-axeln är ampere per fas.
X-axeln är tid i sekunder.
Linjerna representerar vilken huvudsäkring de rekommenderar, röd linje är 16A.
Plupparna är uppmätta värden per fas.
Jo, men tanken var ju att slippa försöka läsa ur värden ur diagrammen med all den brist på avläsningsprecision som det innebär.X xxargs skrev:
Men visst kan jag göra som du skriver, jag ville bara först kolla om det fanns t.ex. tabeller eller någon funktion.
Sen är ju diagrammen olika för olika säkringsfabrikat, säkringstyper och märkström, så jag förstår ju att det även finns en svårighet där.
Det där var spännande.X xxargs skrev:
Ska verkligen inte smälttrådens egen massa samt sanden den ligger i, jämna ut värmetopparna när det är 1 hundradels sekund mellan ...
Mina loggers mäter crestfaktor .
På den exempelfil jag kört med så är crestfaktorn för spänning i princip 1,41 (1,40-1,42), så den är "perfekt".
Crestfaktorn för ström når 2 ibland (under natten då det går lägre ström totalt), och det är ju inte heller speciellt svårt. Men det är kanske något att hålla koll på ...
Här är XL-arket i nuvarande form, så långt som jag kommit.
Det finns en del som sköts automagiskt, t.ex. att arket själv räknar ut hur många rader dataserien är, man behöver inte kolla detta och fylla i någonstans.
Jag skulle gärna sett att diagrammen också fixade gränserna själva, men jag har inte kommit på hur man gör.
Det skulle också kunna varit trevligt att ha en kontroll av något slag, eller en ruta att fylla i ett värde, så man justerade lite beroende på vilka säkringsstorlekar man rör sig med.
Det kanske fixas förbättringar vad det lider ...
Det finns en del som sköts automagiskt, t.ex. att arket själv räknar ut hur många rader dataserien är, man behöver inte kolla detta och fylla i någonstans.
Jag skulle gärna sett att diagrammen också fixade gränserna själva, men jag har inte kommit på hur man gör.
Det skulle också kunna varit trevligt att ha en kontroll av något slag, eller en ruta att fylla i ett värde, så man justerade lite beroende på vilka säkringsstorlekar man rör sig med.
Det kanske fixas förbättringar vad det lider ...
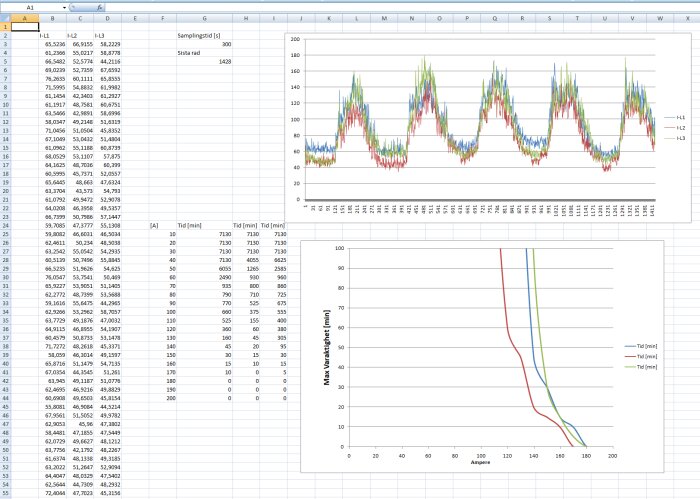
Jag slänger in två skärmdumpar också.
Den första visar hela mätperiodens alla samplingar och sen ett diagram som visar längsta varaktighet i minuter för en viss nivå på strömmen.
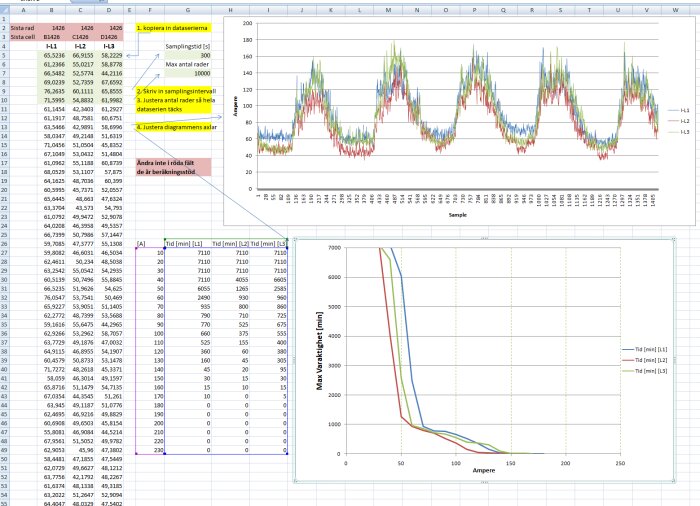
Sen zoomar jag in lite i diagram 2, då det är ganska ointressant att se att t.ex. vid 35A så blir det hela mätperioden, då strömmen aldrig blir mindre.
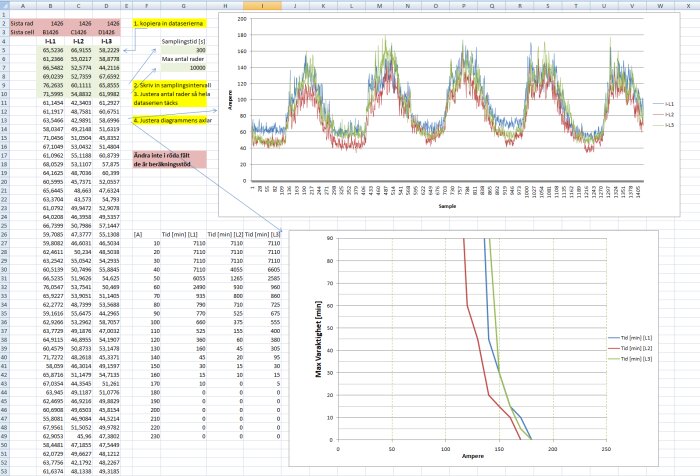
Det intressanta är att se hur långa perioder det är med hög ström, så med Y-axeln på 90 minuter så går det att bättre se hur mycket ström det går under t.ex. 5 minuter eller 10 minuter etc.
Den första visar hela mätperiodens alla samplingar och sen ett diagram som visar längsta varaktighet i minuter för en viss nivå på strömmen.
Sen zoomar jag in lite i diagram 2, då det är ganska ointressant att se att t.ex. vid 35A så blir det hela mätperioden, då strömmen aldrig blir mindre.
Det intressanta är att se hur långa perioder det är med hög ström, så med Y-axeln på 90 minuter så går det att bättre se hur mycket ström det går under t.ex. 5 minuter eller 10 minuter etc.
Jag tycker faktiskt att det finns något pedagogiskt attraktivt i det som NICHOLAS J visade.NICHOLAS J skrev:
Jag förstår det som att plupparna är olika tid vs ström, grupperade på något vis (typ 9A till 10A och mellan 1 och 2 minuter varaktighet), typ så.
Och jag sitter och kikar på bilden, och tänker att den orangea, L2, har mycket förbrukning på ca 1 minuts längd och ca 8-9 A, dvs många prickar här.
Och då tänker jag vidare, kanske en vattenkokare, typiskt förbrukningsmönster för en sådan.
Medan L1 har något som ofta drar ca 17A, ibland kortare tid, ibland lång tid.
(Ja det kan ju självklart vara olika laster också, som ibland blir samtidigt sådär)
Men jag gillar pedagogiken i bilden, prickarna som visar på ström i olika tidsintervall ska helt enkelt befinna sig under linjen för vad säkringen klarar.
Enkelt att förstå, en bra visualisering.
Verkligheten, angående hur ofta man tar ut max.
3 gånger på 16 år fick jag byta en huvudsäkring i vår villa på 120 kvm med 16A.
Det var 16A när vi köpte huset, det var bara använt som sommarboende, om vi ville byta till högre huvudsäkring behövde vi även byta kabeln in i huset från stolpen, så jag hoppade över det. Vattenfall sa att vårt hus behövde 25A när vi tecknade abonnemang för permanentboende.
Alla element 400v 2 fas drog jag själv och fas balanserade, varmvattenberedaren var 3 fas.
2 gånger när proppen gick var det smällkallt ute hade sambon dragit igång hela tvättstugan och diskmaskinen, ungarna hade badat, jag hade 2,5 kw värmefläkten på i garaget och så startade kompressorn.
Den 3e gången var det samma sak, men då startade sambon dammsugaren när proppen gick.
Vi hade även en luftvärmepump 1100w , och det var fasen som den var kopplad till som proppen gick.
3 gånger på 16 år fick jag byta en huvudsäkring i vår villa på 120 kvm med 16A.
Det var 16A när vi köpte huset, det var bara använt som sommarboende, om vi ville byta till högre huvudsäkring behövde vi även byta kabeln in i huset från stolpen, så jag hoppade över det. Vattenfall sa att vårt hus behövde 25A när vi tecknade abonnemang för permanentboende.
Alla element 400v 2 fas drog jag själv och fas balanserade, varmvattenberedaren var 3 fas.
2 gånger när proppen gick var det smällkallt ute hade sambon dragit igång hela tvättstugan och diskmaskinen, ungarna hade badat, jag hade 2,5 kw värmefläkten på i garaget och så startade kompressorn.
Den 3e gången var det samma sak, men då startade sambon dammsugaren när proppen gick.
Vi hade även en luftvärmepump 1100w , och det var fasen som den var kopplad till som proppen gick.