4 640 läst · 49 svar
5k läst
49 svar
Hjälp med excel, räkna på huvudsäkring
Kanske redan har sagts men är det inte egentligen så pass enkelt som såhär:
Glidande medelvärde bildas över några tidsperioder, t.ex. 1s, 10s, 60s, 10min, 30min, 60min.
För varje period så bestämmer man ett gränsvärde som inte får överskridas någon gång, detta baseras då på säkringens storlek och karakteristik.
Exakt hur man gör detta i Excel kan jag inte säga på rak arm, men ge mig rådatan så kan jag skriva ett pythonscript på några minuter. Har hört att Excel numera stöder inbäddad python så det borde funka där direkt också.
EDIT: För att bättre efterlikna hur varm säkringen blir så är troligend det bästa att använda något form av exponentiellt viktat glidande medelvärde. Alltså ett glidande medelvärde där de ingående värdena (de inom fönstret) viktas beroende på hur länge sedan de inträffade.
Glidande medelvärde bildas över några tidsperioder, t.ex. 1s, 10s, 60s, 10min, 30min, 60min.
För varje period så bestämmer man ett gränsvärde som inte får överskridas någon gång, detta baseras då på säkringens storlek och karakteristik.
Exakt hur man gör detta i Excel kan jag inte säga på rak arm, men ge mig rådatan så kan jag skriva ett pythonscript på några minuter. Har hört att Excel numera stöder inbäddad python så det borde funka där direkt också.
EDIT: För att bättre efterlikna hur varm säkringen blir så är troligend det bästa att använda något form av exponentiellt viktat glidande medelvärde. Alltså ett glidande medelvärde där de ingående värdena (de inom fönstret) viktas beroende på hur länge sedan de inträffade.
Redigerat:
Japp.V vectrex skrev:Kanske redan har sagts men är det inte egentligen så pass enkelt som såhär:
Glidande medelvärde bildas över några tidsperioder, t.ex. 1s, 10s, 60s, 10min, 30min, 60min.
För varje period så bestämmer man ett gränsvärde som inte får överskridas någon gång, detta baseras då på säkringens storlek och karakteristik.
Exakt hur man gör detta i Excel kan jag inte säga på rak arm, men ge mig rådatan så kan jag skriva ett pythonscript på några minuter. Har hört att Excel numera stöder inbäddad python så det borde funka där direkt också.
EDIT: För att bättre efterlikna hur varm säkringen blir så är troligend det bästa att använda något form av exponentiellt viktat glidande medelvärde. Alltså ett glidande medelvärde där de ingående värdena (de inom fönstret) viktas beroende på hur länge sedan de inträffade.
Det där är väl första delen av uppgiften, sen ska man vaska fram worst case också, ifrån en dataserie som börjar likna en sinusvåg efter att ha filtrerats av ett glidande medelvärde.
Jag kan skrivaMikael_L skrev:
=COUNT(E2:E1000)
Då returneras antalet rader med tal i arrayen E2:E1000. (och det är lätt att räkna ut var sista raden då är)
Dock måste jag ta till 1000 mer, dvs så att alla tänkbara storlekar på loggdata ryms ...
Nu har jag kommit en bit påväg.
Såhär ser det ut nu.
Jag har lagt in en riktig och verklig mätserie, som är mätt mån-fre, och som ni kan se på amperen så är det liksom ingen villa, utan det är en fastighet med affärer i.
Mätserien är 1428 samples lång, loggning var 5'e minut, och jag har valt max-värden på I (max inom varje 5-minuters period, kollar jag 1-sekunds data så är de ju inte 5 minuter långa i varaktighet, dessa toppar).
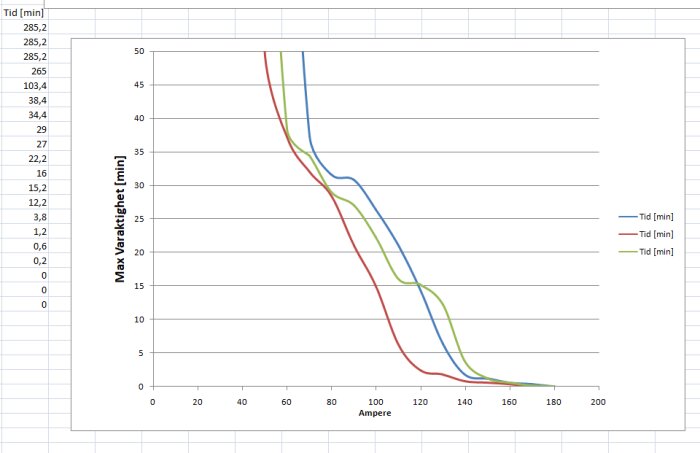
Jag har lagt in mätningen i en graf som är enkel att förstå.
Men den nedre grafen visar max varaktighet för olika max ström, kanske inte helt intuitivt att förstå, men det blir nog ändå bra att utvärdera såhär.
Denna del är rakt av stulen från harkas förslag, utom grafen som jag filat fram själv.
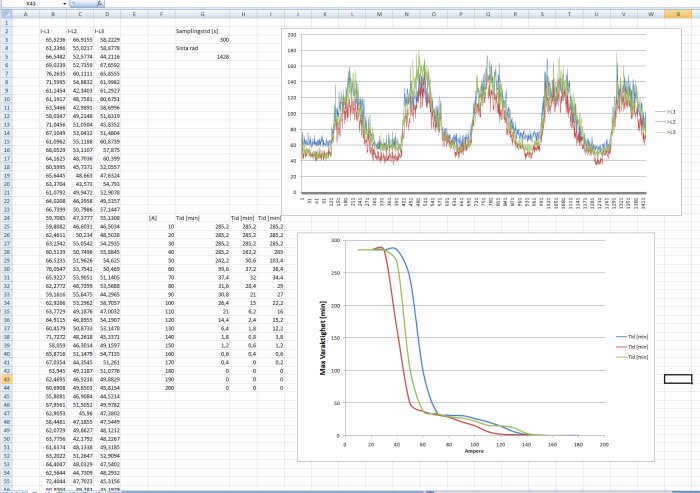
Såhär ser det ut nu.
Jag har lagt in en riktig och verklig mätserie, som är mätt mån-fre, och som ni kan se på amperen så är det liksom ingen villa, utan det är en fastighet med affärer i.
Mätserien är 1428 samples lång, loggning var 5'e minut, och jag har valt max-värden på I (max inom varje 5-minuters period, kollar jag 1-sekunds data så är de ju inte 5 minuter långa i varaktighet, dessa toppar).
Jag har lagt in mätningen i en graf som är enkel att förstå.
Men den nedre grafen visar max varaktighet för olika max ström, kanske inte helt intuitivt att förstå, men det blir nog ändå bra att utvärdera såhär.
Denna del är rakt av stulen från harkas förslag, utom grafen som jag filat fram själv.

Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder
Detta läser jag alltså ut som att om jag har en 160A säkring, så kommer aldrig strömmen vara över 160A i mer än ca 1 minut.
Om jag sätter in en 125A säkring, så kommer strömmen ibland vara över 125A i bortåt 15 minuter (för L1 och L3).
Men då en 125A säkring rätt säkert klarar 125*1,5 = 187,5 A i minst 5 minuter, så kan jag se i diagrammet att det aldrig blir mer än 1 minuts varaktighet vid 187A.
Om jag sätter in en 125A säkring, så kommer strömmen ibland vara över 125A i bortåt 15 minuter (för L1 och L3).
Men då en 125A säkring rätt säkert klarar 125*1,5 = 187,5 A i minst 5 minuter, så kan jag se i diagrammet att det aldrig blir mer än 1 minuts varaktighet vid 187A.
Jag skulle gissa att du tänker på standardavvikelse? Det är ett ganska bra verktyg ifall du vill komplettera data för att få en mer korrekt bild av en dataserie.
Standardavvikelsens nytta kan visas genom ett exempel där en förälder får en inbjudan till en fest. För att förstå vilken sorts fest det handlar om frågar sig föräldern vilken medelålder det är på deltagarna. Svaret blir 40år. När föräldern dyker upp på festen möts den av massa små barn och väldigt många gamlingar, men ingen människa som är 40år.
Med hjälp av en standardavvikelse hade föräldern fått data som sagt att detta värde om 40år har en standardavvikelse på +- 35år.
I excel heter den stdav.
Standardavvikelsens nytta kan visas genom ett exempel där en förälder får en inbjudan till en fest. För att förstå vilken sorts fest det handlar om frågar sig föräldern vilken medelålder det är på deltagarna. Svaret blir 40år. När föräldern dyker upp på festen möts den av massa små barn och väldigt många gamlingar, men ingen människa som är 40år.
Med hjälp av en standardavvikelse hade föräldern fått data som sagt att detta värde om 40år har en standardavvikelse på +- 35år.
I excel heter den stdav.
Det beror väl också på om man ska säkra upp eller ner. Ska du säkra upp så är ju frågan mest om du blåst säkringar eller får varningar från HAN/P1-mätaren ofta att du överskrider säkringen.Mikael_L skrev:
Så jag antar det handlar om att säkra ner. Och då handlar det väl ofta om att en specifik fas är överbelastad och då vore det nog bra att ha 2 grafer: 1 med kombinerad effekt/ström på alla faser och 1 med den högst belastade fasen. Själv klarar jag mig på 16A - den enda säkringen som går är köket med air fryer och vattenkokare samtidigt avsäkrat med 10A så jag behöver nog inte fundera på att byta storlek...
Sen får du väl använda värden från standardavvikelsen och göra en restanalys samt kolla homoskedacitetsvärden. Om jag förstod dig rätt är du endast intresserad av avvikelser från en fastslagen modell där tidsrymden avgör huruvida ett värde är relevant?
Problemet du får med att beräkna glidande medelvärde är just det du själv sagt tidigare, den fångar helt enkelt inte upp toppar och bottnar på samma sätt. Om du istället kan se hur stor avvikelse du har under en given tid, då kommer också denna graf kunna berätta var du befinner dig just i det ögonblicket, inte det samlade värdet från senaste två minuterna.
Problemet du får med att beräkna glidande medelvärde är just det du själv sagt tidigare, den fångar helt enkelt inte upp toppar och bottnar på samma sätt. Om du istället kan se hur stor avvikelse du har under en given tid, då kommer också denna graf kunna berätta var du befinner dig just i det ögonblicket, inte det samlade värdet från senaste två minuterna.
Redigerat:
Får ni till detta så känns det väl ändå som att valfri apptillverkare borde implementera det och kunna erbjuda tjänsten ”spar pengar på abonnemanget! Välj rätt huvudsäkring tack vare vår avancerade algoritm som bedömer vad du faktiskt behöver” tillsammans med valfri homewizard, logger etc..
det ser väl bra ut!Mikael_L skrev:
Nu har jag kommit en bit påväg.
Såhär ser det ut nu.
Jag har lagt in en riktig och verklig mätserie, som är mätt mån-fre, och som ni kan se på amperen så är det liksom ingen villa, utan det är en fastighet med affärer i.
Mätserien är 1428 samples lång, loggning var 5'e minut, och jag har valt max-värden på I (max inom varje 5-minuters period, kollar jag 1-sekunds data så är de ju inte 5 minuter långa i varaktighet, dessa toppar).
Jag har lagt in mätningen i en graf som är enkel att förstå.
Men den nedre grafen visar max varaktighet för olika max ström, kanske inte helt intuitivt att förstå, men det blir nog ändå bra att utvärdera såhär.
Denna del är rakt av stulen från harkas förslag, utom grafen som jag filat fram själv.
[bild]
men jag får inte ihop enheterna i tabellen/grafen – om samplingstiden än 5 minuter, hur får du resultat som 0.4 minuter? eller att hela mätperioden (I > 10A) skulle vara 285.2 minuter lång (knappt fem timmar)... ska tiderna i tabell/graf multipliceras med 24?
Jag kan fråga dig igen kan du inte göra något likt det jag beskrev i #7? Då är vi direkt lite mer på spår och åtminstone lite realistiskt användbart för många olika fall.harka skrev:
kör man excel med engelska regionalsättningar så har excel kommatecken som separator – men med svenska regionalsättningar används semikolon (eftersom vi använder kommatecknet till decimalkomma) – AND(förvirrande; irriterande)
har man aldrig använt array formulas så matas dessa inte in med en enkel enter-tryckning utan med en trefingerstryckning: Ctrl-Shift-Enter och formeln kommer då att omges av måsvingar: {=MAX(FREQUENCY(IF($H$5:...))))}
man ska alltså inte själv knappa in måsvingarna