8 522 läst · 54 svar
9k läst
54 svar
Beräkna var daggpunkten hamnar ?
Tack för redogörelsen, jag tycker allt du skriver verkar rimligt. Tycker du resultatet av min simulering i #30 ser rimlig ut ? Den bekräftar dessvärre min teori om det är korrekt.
hlph skrev:
Jag kommer inte att kunna lösa dina problem, men jag vill gärna ge några teoretiska kommentarer, som förhoppningsvis kan ge ytterligare lite förståelse av hur det fungerar.
Det här är ett typiskt stationärt värmeledningsproblem. Värmeledningsproblemet styras av en differentialekvation som talar om hur värmen sprids i en kropp utifrån den energi vi tillför. Sen behövs en, som det heter, konstitutiv lag som kopplar ihop energiflöde med en temperaturgradient, förenklat en temperaturskillnad. Den lag man brukar använda är Fouriers lag, den säger att energiflödet är proportionellt mot temperaturgradienten. Proportionalitetskoefficienten är värmekonduktiviteten, lambda är nämnt tidigare i tråden. Om man då tar ett enkelt exempel, en vägg i samma material. Genom den väggen har man en viss energiförlust, då kommer värmeledningsekvationen och Fouriers lag att ge att temperaturen varierar linjärt genom väggens tjocklek. Jag har sätt motsvarande resonemang i tråden för rörisoleringen. Problemet är att vi har inte ett så enkelt fall. Vi har ett rör och isolering med cirkulärt tvärsnitt. Jag tror att det är enklast att tänka sig att vi tittar på energiflödet genom ett snitt som ser ut som en tårtbit. Energin som går in längst in vid spetsen (ytan på röret) ska vara lika stor som den som går ut vid kanten (ytterytan på isoleringen). Eftersom arean vid kanten är mycket större än arean vid spetsen så kommer energiflödet per areaenhet att minska när vi går från ytan på röret till ytterytan på isoleringen. Men Fouriers lag gäller fortfarande, dvs. energiflödet per areaenhet är proportionell mot temperaturgradienten. För att få ihop det här så måste temperatur variera olinjärt genom isoleringen, temperaturgradienten kommer att minska ju lägre ut man kommer. Man kan ju då fråga sig, kan man inte approximera det med en linjär temperaturvariation? Det skulle man med gott samvete kunna om isoleringen var tunn, men det är den inte, så det är tveksamt att göra den typen av approximation.
Nästa sak jag läst i tråden är diskussioner om vad isoleringen kommer att ha för yttemperatur. Isoleringen kommer inte att ha samma temperatur som omgivande luft. Det som ger värmeöverföringen mellan ytterytan på isoleringen och luften är till största delen konvektion. Man brukar anta att ett konvektionsrandvillkor styrs av att energiflödet genom ytan är proportionellt mot skillnaden mellan yttemperaturen och temperatur på omgivande luft. Proportionalitetskoefficienten är tyvärr knepig att få fram. Den beror på ytbeskaffenhet och definitivt på lufthastigheten. Om luften är stillastående så har man naturlig konvektion. Då kommer uppvärmning av luften vid ytan ge upphov till rörelse i luften.
Det var några kommentarer, det kanske förvirrar mer, men jag tycker ändå att man ska vara försiktig med alltför grova förklaringsmodeller och antaganden.
Redigerat:
Jag har suttit ett tag och funderat på resultatet. Jag jobbar normalt sätt inte med analys av värmeledningsproblem. Jag håller på med hållfasthetsanalyser, men det händer att jag även räknar på värmeledning. Jag har dock rätt bra kunskaper om teorierna bakom. Det är inte så konstigt att lambda, densitet och värmekapacitet inte påverkar. Densitet och värmekapacitet kommer bara in om man har ett transit förlopp, dvs. att förhållandena ändras med tiden, t.ex. vid en uppvärmning. I det här fallet har vi ett steady state tillstånd. lambda kommer inte in i just din modell eftersom du har specificerat temperaturer på alla ytor. Den kommer in om man har en given effektkälla eller konvektionsrandvillkor.frma71 skrev:
Egentligen tror jag att det är en väl grov approximation att ansätta 25 grader på ytterytorna. Om rören ligger i ett bjälklag så borde nog golv och tak närmast rören ha någon typ konvektions randvillkor, de lär bli något lite kalla än golv och tak lägra bort från rören, förmodligen rätt lite. Sen om man tittar längs bjälklaget tvärs röret så tror jag att om man kommer en bit bort från rören så sker det inte mycket värmetransport i den riktningen, då skulle man kunna ha isolations randvillkor. Det får man om man inte aktivt sätter några randvillkor i modellen. Men jag tror dock att om man inför lite mer realistiska randvillkor så blir situationen värre, temperaturen i isoleringen kommer att bli lägre. Så om du redan hade för låg temperatur utanför rörisoleringen, så blir det ju inte bättre.
Det är ju högst relevanta funderingar du har. Det blir kanske bättre att bara ha rörisolering och sen luft runt som kan cirkulera lite? Jag ska fundera lite till på det här, det är ett intressant problem.
Tack, jo sjukt mycket mer komplicerat än jag trodde från början. Håller på och kör en simulering med konvektion nu också.
Håller med, det är inte konstigt att det inte påverkar jämviktsläget.
Håller också med om att modellen är förenklad. Men som du skriver är den förenklar på ett sådant sätt att får man inte godtagbara resultat med dom lär man inte få det med en mer exakt modell.
/Fredrik
Håller med, det är inte konstigt att det inte påverkar jämviktsläget.
Håller också med om att modellen är förenklad. Men som du skriver är den förenklar på ett sådant sätt att får man inte godtagbara resultat med dom lär man inte få det med en mer exakt modell.
/Fredrik
hlph skrev:
Jag har suttit ett tag och funderat på resultatet. Jag jobbar normalt sätt inte med analys av värmeledningsproblem. Jag håller på med hållfasthetsanalyser, men det händer att jag även räknar på värmeledning. Jag har dock rätt bra kunskaper om teorierna bakom. Det är inte så konstigt att lambda, densitet och värmekapacitet inte påverkar. Densitet och värmekapacitet kommer bara in om man har ett transit förlopp, dvs. att förhållandena ändras med tiden, t.ex. vid en uppvärmning. I det här fallet har vi ett steady state tillstånd. lambda kommer inte in i just din modell eftersom du har specificerat temperaturer på alla ytor. Den kommer in om man har en given effektkälla eller konvektionsrandvillkor.
Egentligen tror jag att det är en väl grov approximation att ansätta 25 grader på ytterytorna. Om rören ligger i ett bjälklag så borde nog golv och tak närmast rören ha någon typ konvektions randvillkor, de lär bli något lite kalla än golv och tak lägra bort från rören, förmodligen rätt lite. Sen om man tittar längs bjälklaget tvärs röret så tror jag att om man kommer en bit bort från rören så sker det inte mycket värmetransport i den riktningen, då skulle man kunna ha isolations randvillkor. Det får man om man inte aktivt sätter några randvillkor i modellen. Men jag tror dock att om man inför lite mer realistiska randvillkor så blir situationen värre, temperaturen i isoleringen kommer att bli lägre. Så om du redan hade för låg temperatur utanför rörisoleringen, så blir det ju inte bättre.
Det är ju högst relevanta funderingar du har. Det blir kanske bättre att bara ha rörisolering och sen luft runt som kan cirkulera lite? Jag ska fundera lite till på det här, det är ett intressant problem.
Jo, jag hade en hängslen-och-livremslösning där jag drar den isolerade slangen i VP-rör, då skulle man ju kunna tvinga fram rörelse om man måste. Jag tror iofs det skulle bli rätt ok självdrag då jag bara kyler på övervåningen.
/Fredrik
/Fredrik
hlph skrev:
Jag har suttit ett tag och funderat på resultatet. Jag jobbar normalt sätt inte med analys av värmeledningsproblem. Jag håller på med hållfasthetsanalyser, men det händer att jag även räknar på värmeledning. Jag har dock rätt bra kunskaper om teorierna bakom. Det är inte så konstigt att lambda, densitet och värmekapacitet inte påverkar. Densitet och värmekapacitet kommer bara in om man har ett transit förlopp, dvs. att förhållandena ändras med tiden, t.ex. vid en uppvärmning. I det här fallet har vi ett steady state tillstånd. lambda kommer inte in i just din modell eftersom du har specificerat temperaturer på alla ytor. Den kommer in om man har en given effektkälla eller konvektionsrandvillkor.
Egentligen tror jag att det är en väl grov approximation att ansätta 25 grader på ytterytorna. Om rören ligger i ett bjälklag så borde nog golv och tak närmast rören ha någon typ konvektions randvillkor, de lär bli något lite kalla än golv och tak lägra bort från rören, förmodligen rätt lite. Sen om man tittar längs bjälklaget tvärs röret så tror jag att om man kommer en bit bort från rören så sker det inte mycket värmetransport i den riktningen, då skulle man kunna ha isolations randvillkor. Det får man om man inte aktivt sätter några randvillkor i modellen. Men jag tror dock att om man inför lite mer realistiska randvillkor så blir situationen värre, temperaturen i isoleringen kommer att bli lägre. Så om du redan hade för låg temperatur utanför rörisoleringen, så blir det ju inte bättre.
Det är ju högst relevanta funderingar du har. Det blir kanske bättre att bara ha rörisolering och sen luft runt som kan cirkulera lite? Jag ska fundera lite till på det här, det är ett intressant problem.
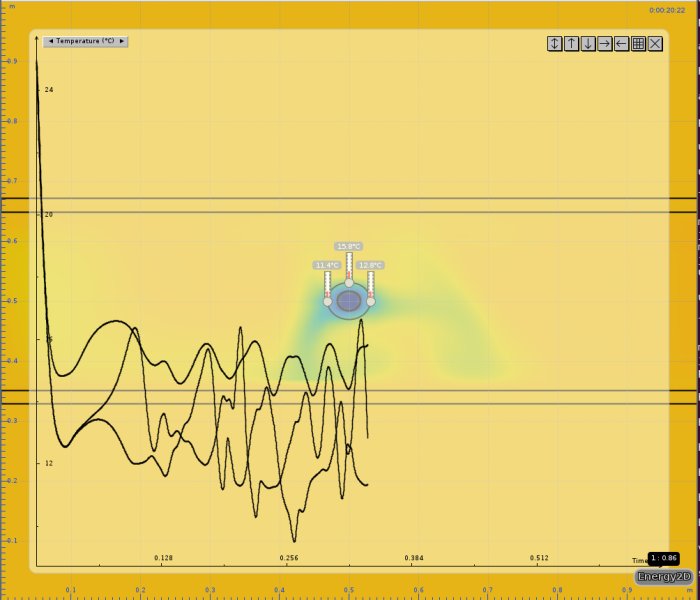
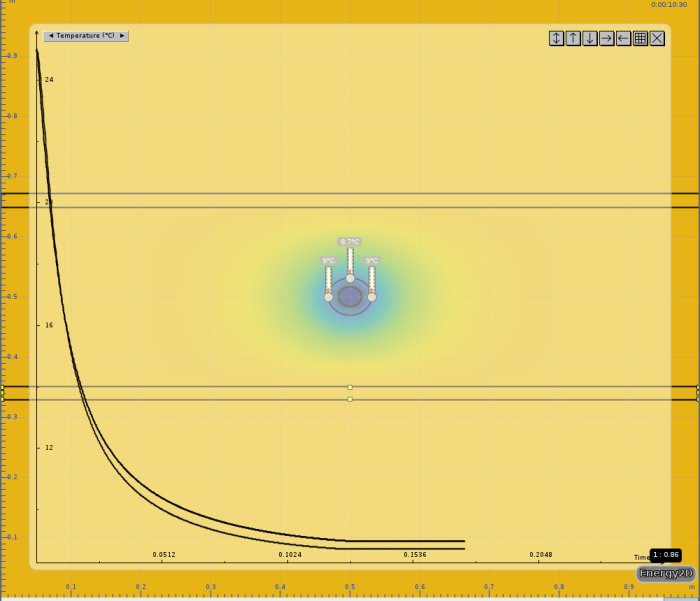
Gjort två nya körningar med luft runt röret, med och utan konvektion. Fortfarande blir det sämre/kallare än paroc:s kalkylator.

Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder

Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder
Sen behöver det ju inte bli kondens bara för att temperaturen är några grader under daggpunkten. Vattenångan rör sig mot luft med lägre ångtryck, dvs mot den varmare luften, så närmast röret blir ånghalten lägre så länge det inte är luftväxling.
Hmm, det är ju också en aspekt som bör bidra positivt.
/Fredrik
/Fredrik
useless skrev:
I princip stämmer det. Kan bidra med ett praktiskt exempel. Vi har precis bytt en hel yttervägg som blivit helt förstörd på grund av ett frysrum på insidan av väggen. Oavsett hur bra isolerat frysrummet är måste du ha luftcirkulation eller värmeslinga för att undvika att daggpunkten hamnar i ytterväggen. Men i ett bjälklag har du ju ett hyfsat kontrollerat omgivningsklimat med avseende på luftfuktighet.frma71 skrev:
Tack för svar, tror det kan vara en lösning att dra dom isolerade brine-rören i vp-rör så man kan kan få ett luftflöde runt dom ? Då tar man ju dessutom tillvara den kyla som läcker ut genom isoleringen.
/Fredrik
/Fredrik
C cpalm skrev:I princip stämmer det. Kan bidra med ett praktiskt exempel. Vi har precis bytt en hel yttervägg som blivit helt förstörd på grund av ett frysrum på insidan av väggen. Oavsett hur bra isolerat frysrummet är måste du ha luftcirkulation eller värmeslinga för att undvika att daggpunkten hamnar i ytterväggen. Men i ett bjälklag har du ju ett hyfsat kontrollerat omgivningsklimat med avseende på luftfuktighet.
Bästa svaret
Jag har tittat lite på vad Paroc gör, de fler ju standarden EN ISO 12241, den beskriver bland annat hur man räknar på värmeförluster på rör. Den utgår från färdiga uttryck för temperaturfördelningar och värmetransporter. Utöver temperatur randvillkor så tar man med konvektion och strålning. Men det här är inget annat än färdiga lösningar på värmeekvation, som man annars för godtyckliga geometrier t.ex.kan lösa med finita element metoden.frma71 skrev:
Jag gjorde en snabb beräkning på ett rör med de data du har gett. Jag lät röret ligga fritt i luft (inget som stänger in luften) jag satte temperaturrandvillkor på innerytan och konvektion på ytterytan. Då fick jag att temperaturen gick från 2 grader till 20 grader på isoleringens ytteryta, vilket väl är rätt likt vad man får om man använder Parocs beräkningsprogram. Det är dock inte säkert att den här analysen är realistisk för vad som händer när man har rören i ett instängt bjälklag.
Jag har tittat lite närmare på dina senaste analyser, de med och utan konvektion. Jag tycker att resultaten är lite märkliga, men det är nog så att jag förstår inte riktigt hur du har satt upp modellerna.
Hej och tack. Jag har använt Energy 3D (https://energy.concord.org/energy2d/) vilket verkar vara resultatet av något forskningsprojekt, initialt verkade det fungera bra. Men jag börjar tvivla på resultaten från programmet, men ska prova köra några vändor till med högre tidsupplösning.
Vad har du räknat med ? Förenklingarna från EN ISO 12241 eller har du någon mer professionell mjukvara för FEM-analysen ?
Vad har du räknat med ? Förenklingarna från EN ISO 12241 eller har du någon mer professionell mjukvara för FEM-analysen ?
hlph skrev:
Jag har tittat lite på vad Paroc gör, de fler ju standarden EN ISO 12241, den beskriver bland annat hur man räknar på värmeförluster på rör. Den utgår från färdiga uttryck för temperaturfördelningar och värmetransporter. Utöver temperatur randvillkor så tar man med konvektion och strålning. Men det här är inget annat än färdiga lösningar på värmeekvation, som man annars för godtyckliga geometrier t.ex.kan lösa med finita element metoden.
Jag gjorde en snabb beräkning på ett rör med de data du har gett. Jag lät röret ligga fritt i luft (inget som stänger in luften) jag satte temperaturrandvillkor på innerytan och konvektion på ytterytan. Då fick jag att temperaturen gick från 2 grader till 20 grader på isoleringens ytteryta, vilket väl är rätt likt vad man får om man använder Parocs beräkningsprogram. Det är dock inte säkert att den här analysen är realistisk för vad som händer när man har rören i ett instängt bjälklag.
Jag har tittat lite närmare på dina senaste analyser, de med och utan konvektion. Jag tycker att resultaten är lite märkliga, men det är nog så att jag förstår inte riktigt hur du har satt upp modellerna.
jag hade kört det här som ett stationärt problem, dvs inga tidsberoenden. Jag använder ett kommersiellt finita element program. Om du gjort en transient analys så förklarar det varför vissa kurvor är så svängiga. Jag undrar hur du har modellerat luften? För jag tolkade det som att du modellerat den på något sätt och fått ut en temperaturfördelning i luften.frma71 skrev:
Hej och tack. Jag har använt Energy 3D ([länk]) vilket verkar vara resultatet av något forskningsprojekt, initialt verkade det fungera bra. Men jag börjar tvivla på resultaten från programmet, men ska prova köra några vändor till med högre tidsupplösning.
Vad har du räknat med ? Förenklingarna från EN ISO 12241 eller har du någon mer professionell mjukvara för FEM-analysen ?
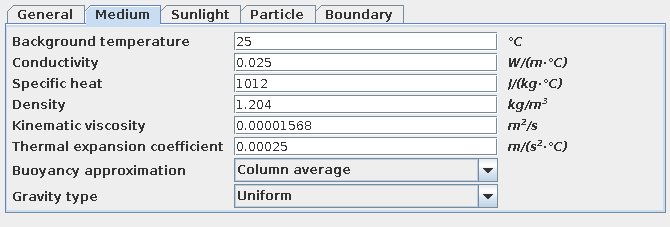
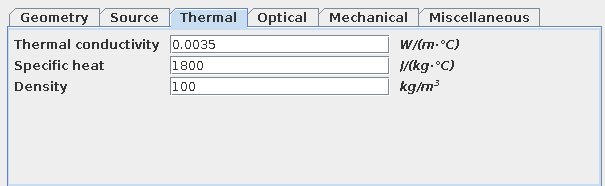
Oklart för mig, programmet (Energy 2D) hade följande förinställda parametrar, dubbelkollade några och det verkar vara luft.

hlph skrev:
jag hade kört det här som ett stationärt problem, dvs inga tidsberoenden. Jag använder ett kommersiellt finita element program. Om du gjort en transient analys så förklarar det varför vissa kurvor är så svängiga. Jag undrar hur du har modellerat luften? För jag tolkade det som att du modellerat den på något sätt och fått ut en temperaturfördelning i luften.
En sak jag gjort sen jag postade bilderna ovan var att uppdatera värmekapacitiviteten för isoleringen. Jag tänkte först att den och densiteten inte spelade någon roll då det var värdena i det stabila tillståndet jag var ute efter. Med högre värmekapacitivitet blev allt mycket stabilare. Nu har jag:

hlph skrev:
jag hade kört det här som ett stationärt problem, dvs inga tidsberoenden. Jag använder ett kommersiellt finita element program. Om du gjort en transient analys så förklarar det varför vissa kurvor är så svängiga. Jag undrar hur du har modellerat luften? För jag tolkade det som att du modellerat den på något sätt och fått ut en temperaturfördelning i luften.