Nej, det är en högst praktisk fråga. Ska installera frikyla och ville försäkra mig om att jag inte får kondens då brine-rören ska dras genom bjälklaget.
Jo, jag är en kontrollfreak som har svårt att lita på folk, särskilt rörmokare (på grund av tidigare erfarenheter)
Jo, jag är en kontrollfreak som har svårt att lita på folk, särskilt rörmokare (på grund av tidigare erfarenheter)
Jarlingar skrev:
15 mm isolering med lambda 0,04 kommer ha en yttemperatur på ca +19,5° på utsidan och ca +3,7° på insida (mot rör).
Mättnadsånghalten för +19,5° motsvara ca 73%RF vid +25°
VIKTIGT att du väljer en diffusionstät isolering typ Armaflex eller motsv.
Mättnadsånghalten för +19,5° motsvara ca 73%RF vid +25°
VIKTIGT att du väljer en diffusionstät isolering typ Armaflex eller motsv.
Man räknar med övergångsmotstånd, jag har pluggat en hel del fukt.. Fuktsakkunnig.
Spelar ingen roll om du har ytterligare lösull runt röret ur fuktsynpunkt.
Med vald slang klarar du dig som sagt utan kondensutfällning upp till ca 73%RF vid +25° om kylmediet är +2°
Spelar ingen roll om du har ytterligare lösull runt röret ur fuktsynpunkt.
Med vald slang klarar du dig som sagt utan kondensutfällning upp till ca 73%RF vid +25° om kylmediet är +2°
Ok jag är tacksam för infon och ifrågasätter dig inte, jag vill bara förstå.
Rent logiskt borde ju rörets yta bli kallare om jag isolerar mer utanför röret (med isolering som inte är diffusionstät) med risk för kodens, eller har det här med energin som går åt för att kondensera vattenångan att göra (ångbildningsentalpi ?).
Om du orkar får du gärna förklara hur man tänker/räknar eller referera till något jag kan läsa, jag är hyffsad på matte och fysik i allmänhet men ingen konstruktör eller byggare.
Rent logiskt borde ju rörets yta bli kallare om jag isolerar mer utanför röret (med isolering som inte är diffusionstät) med risk för kodens, eller har det här med energin som går åt för att kondensera vattenångan att göra (ångbildningsentalpi ?).
Om du orkar får du gärna förklara hur man tänker/räknar eller referera till något jag kan läsa, jag är hyffsad på matte och fysik i allmänhet men ingen konstruktör eller byggare.
Eller säg så här. Jag har samma rör, samma temperarurer. Men jag har 15mm diffusionstät isolering och ytterligare 135mm icke diffusionstät isolering. För enkelhets skull samma lambda. Vi antar ett stort löftflöde så att utsidan av den yttre isoleringen är 25 grader.
Då kommer det väl att vara 2+(25-2)*(15/150) = 4.3 grader på ytan av den inre isoleringen ? och risk för kondens i den yttre isoleringen ?
Vad är det jag missar ?
Förklaring av beräkningen ovan:
Tx = temperatur på ytan av den inre isoleringen.
Tk = köldbörartemp (2 C)
To = omgivningstemp (25 C)
ti = tjocklek på inre isolering (15mm)
ty = tjocklek på yttre isolering (135mm)
Tx = Tk + (To-Tk)*(ti/(ti+ty))
/Fredrik
Då kommer det väl att vara 2+(25-2)*(15/150) = 4.3 grader på ytan av den inre isoleringen ? och risk för kondens i den yttre isoleringen ?
Vad är det jag missar ?
Förklaring av beräkningen ovan:
Tx = temperatur på ytan av den inre isoleringen.
Tk = köldbörartemp (2 C)
To = omgivningstemp (25 C)
ti = tjocklek på inre isolering (15mm)
ty = tjocklek på yttre isolering (135mm)
Tx = Tk + (To-Tk)*(ti/(ti+ty))
/Fredrik
Rörets yta kommer aldrig bli kallare än köldmediet.
Det är +2° yttemperatur på röret jag har räknat med.
Redigerat:
Njae, I anslutning till det kalla röret kommer det ju att vara två grader, halvvägs in i isoleringen (armaflex, lösull eller vad det nu kan vara) kommer det vara mitt emellan 2 och 25 etc. Eller tänker jag helt galet ?
Jag vet ju att faktiskt inte är så i verkligheten, kan det ha med kvadratisk utbredning att göra ? Typ all kyla kommer från en litet område, medan värmen kommer från ett stort område ?
Jag vet ju att faktiskt inte är så i verkligheten, kan det ha med kvadratisk utbredning att göra ? Typ all kyla kommer från en litet område, medan värmen kommer från ett stort område ?
Redigerat:
Jag kommer inte att kunna lösa dina problem, men jag vill gärna ge några teoretiska kommentarer, som förhoppningsvis kan ge ytterligare lite förståelse av hur det fungerar.
Det här är ett typiskt stationärt värmeledningsproblem. Värmeledningsproblemet styras av en differentialekvation som talar om hur värmen sprids i en kropp utifrån den energi vi tillför. Sen behövs en, som det heter, konstitutiv lag som kopplar ihop energiflöde med en temperaturgradient, förenklat en temperaturskillnad. Den lag man brukar använda är Fouriers lag, den säger att energiflödet är proportionellt mot temperaturgradienten. Proportionalitetskoefficienten är värmekonduktiviteten, lambda är nämnt tidigare i tråden. Om man då tar ett enkelt exempel, en vägg i samma material. Genom den väggen har man en viss energiförlust, då kommer värmeledningsekvationen och Fouriers lag att ge att temperaturen varierar linjärt genom väggens tjocklek. Jag har sätt motsvarande resonemang i tråden för rörisoleringen. Problemet är att vi har inte ett så enkelt fall. Vi har ett rör och isolering med cirkulärt tvärsnitt. Jag tror att det är enklast att tänka sig att vi tittar på energiflödet genom ett snitt som ser ut som en tårtbit. Energin som går in längst in vid spetsen (ytan på röret) ska vara lika stor som den som går ut vid kanten (ytterytan på isoleringen). Eftersom arean vid kanten är mycket större än arean vid spetsen så kommer energiflödet per areaenhet att minska när vi går från ytan på röret till ytterytan på isoleringen. Men Fouriers lag gäller fortfarande, dvs. energiflödet per areaenhet är proportionell mot temperaturgradienten. För att få ihop det här så måste temperatur variera olinjärt genom isoleringen, temperaturgradienten kommer att minska ju lägre ut man kommer. Man kan ju då fråga sig, kan man inte approximera det med en linjär temperaturvariation? Det skulle man med gott samvete kunna om isoleringen var tunn, men det är den inte, så det är tveksamt att göra den typen av approximation.
Nästa sak jag läst i tråden är diskussioner om vad isoleringen kommer att ha för yttemperatur. Isoleringen kommer inte att ha samma temperatur som omgivande luft. Det som ger värmeöverföringen mellan ytterytan på isoleringen och luften är till största delen konvektion. Man brukar anta att ett konvektionsrandvillkor styrs av att energiflödet genom ytan är proportionellt mot skillnaden mellan yttemperaturen och temperatur på omgivande luft. Proportionalitetskoefficienten är tyvärr knepig att få fram. Den beror på ytbeskaffenhet och definitivt på lufthastigheten. Om luften är stillastående så har man naturlig konvektion. Då kommer uppvärmning av luften vid ytan ge upphov till rörelse i luften.
Det var några kommentarer, det kanske förvirrar mer, men jag tycker ändå att man ska vara försiktig med alltför grova förklaringsmodeller och antaganden.
Det här är ett typiskt stationärt värmeledningsproblem. Värmeledningsproblemet styras av en differentialekvation som talar om hur värmen sprids i en kropp utifrån den energi vi tillför. Sen behövs en, som det heter, konstitutiv lag som kopplar ihop energiflöde med en temperaturgradient, förenklat en temperaturskillnad. Den lag man brukar använda är Fouriers lag, den säger att energiflödet är proportionellt mot temperaturgradienten. Proportionalitetskoefficienten är värmekonduktiviteten, lambda är nämnt tidigare i tråden. Om man då tar ett enkelt exempel, en vägg i samma material. Genom den väggen har man en viss energiförlust, då kommer värmeledningsekvationen och Fouriers lag att ge att temperaturen varierar linjärt genom väggens tjocklek. Jag har sätt motsvarande resonemang i tråden för rörisoleringen. Problemet är att vi har inte ett så enkelt fall. Vi har ett rör och isolering med cirkulärt tvärsnitt. Jag tror att det är enklast att tänka sig att vi tittar på energiflödet genom ett snitt som ser ut som en tårtbit. Energin som går in längst in vid spetsen (ytan på röret) ska vara lika stor som den som går ut vid kanten (ytterytan på isoleringen). Eftersom arean vid kanten är mycket större än arean vid spetsen så kommer energiflödet per areaenhet att minska när vi går från ytan på röret till ytterytan på isoleringen. Men Fouriers lag gäller fortfarande, dvs. energiflödet per areaenhet är proportionell mot temperaturgradienten. För att få ihop det här så måste temperatur variera olinjärt genom isoleringen, temperaturgradienten kommer att minska ju lägre ut man kommer. Man kan ju då fråga sig, kan man inte approximera det med en linjär temperaturvariation? Det skulle man med gott samvete kunna om isoleringen var tunn, men det är den inte, så det är tveksamt att göra den typen av approximation.
Nästa sak jag läst i tråden är diskussioner om vad isoleringen kommer att ha för yttemperatur. Isoleringen kommer inte att ha samma temperatur som omgivande luft. Det som ger värmeöverföringen mellan ytterytan på isoleringen och luften är till största delen konvektion. Man brukar anta att ett konvektionsrandvillkor styrs av att energiflödet genom ytan är proportionellt mot skillnaden mellan yttemperaturen och temperatur på omgivande luft. Proportionalitetskoefficienten är tyvärr knepig att få fram. Den beror på ytbeskaffenhet och definitivt på lufthastigheten. Om luften är stillastående så har man naturlig konvektion. Då kommer uppvärmning av luften vid ytan ge upphov till rörelse i luften.
Det var några kommentarer, det kanske förvirrar mer, men jag tycker ändå att man ska vara försiktig med alltför grova förklaringsmodeller och antaganden.
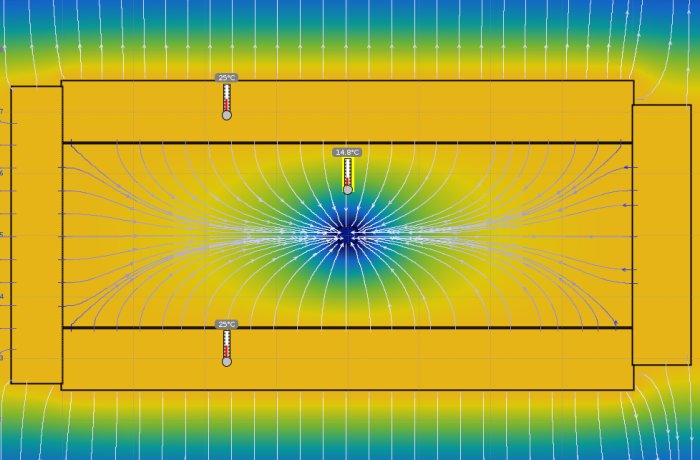
Jag gjorde en simulering i Energy2D som är fritt att använda och gjorde en modell. Bilden visar simuleringen när man i princip nått jämvikt.
Min slutsats är man inte ska lägga brine-rör i isolerade/oventilerade utrymmen om man inte har ångspärr i ytterskikten. Jag hoppas verkligen jag har fel :/
Modellen har fyra block runt omkring som håller en konstant temperatur på 25 grader, sen har den ett block i mitten som har samma egenskaper (lambda, densitet och värmecapacitet) som mineralull. I mitten har den en cirkel som ska motsvarar röret med fast temperatur på 2 grader.
Lambda, densitet och värmecapacitivitet påverkar för övrigt inte jämviktstillståndet alls.
Min slutsats är man inte ska lägga brine-rör i isolerade/oventilerade utrymmen om man inte har ångspärr i ytterskikten. Jag hoppas verkligen jag har fel :/
Modellen har fyra block runt omkring som håller en konstant temperatur på 25 grader, sen har den ett block i mitten som har samma egenskaper (lambda, densitet och värmecapacitet) som mineralull. I mitten har den en cirkel som ska motsvarar röret med fast temperatur på 2 grader.
Lambda, densitet och värmecapacitivitet påverkar för övrigt inte jämviktstillståndet alls.
