Hej,
Jag skulle väldigt gärna få en uppskattning på vad man får för nedböjning på en enkel "konsol" byggd av en HEA balk enligt bild samt vilka "urdragskrafter" det blir i förankringen (röda plåten i bild)?
Det känns inte som en jättekomplicerad beräkning, men jag har googlat och sökt utan att hitta någon bra ledning om hur man går tillväga. Någon som kan hjälpa till med antingen beräkning eller ge lite input på var man kan söka?
Är intresserad av två lastfall enligt bild, 20 resp 10kN. Egentligen är väl även "knäckfallet", dvs. när balken brister intressant, men misstänker att det är såpass högt att det inte är intressant utan den svaga punkten i mitt fall snarast blir infästningen.
Stort tack för all input.
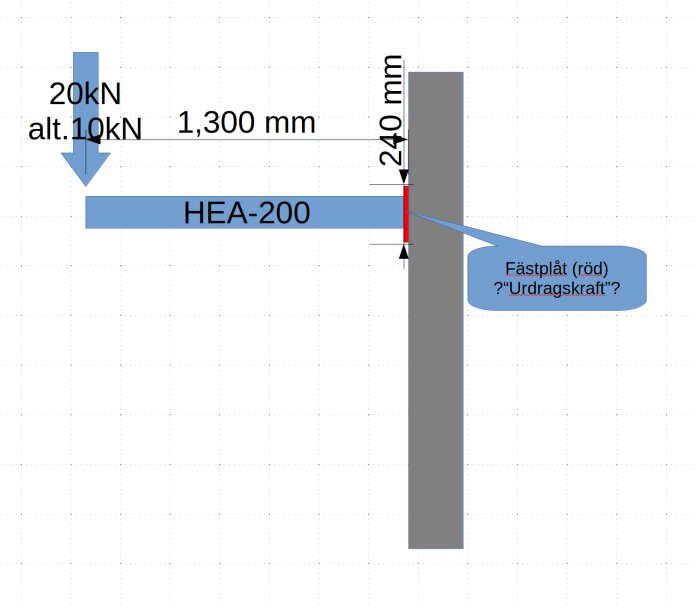
Jag skulle väldigt gärna få en uppskattning på vad man får för nedböjning på en enkel "konsol" byggd av en HEA balk enligt bild samt vilka "urdragskrafter" det blir i förankringen (röda plåten i bild)?
Det känns inte som en jättekomplicerad beräkning, men jag har googlat och sökt utan att hitta någon bra ledning om hur man går tillväga. Någon som kan hjälpa till med antingen beräkning eller ge lite input på var man kan söka?
Är intresserad av två lastfall enligt bild, 20 resp 10kN. Egentligen är väl även "knäckfallet", dvs. när balken brister intressant, men misstänker att det är såpass högt att det inte är intressant utan den svaga punkten i mitt fall snarast blir infästningen.
Stort tack för all input.

Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder
Det är Eurocode 3: Design of steel structures - Part 1-8: Design of joints du ska leta i skulle jag säga. Kapitel 6 rimligtvis. Det är relativt styv materia, både stål och beräkningarna bakom.
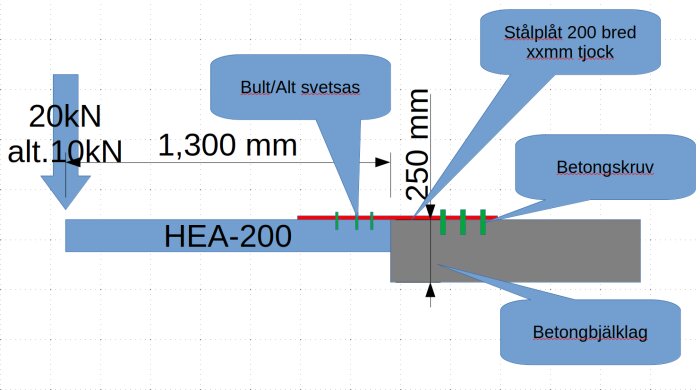
I detta fallet är ju inget gjort, så dessa detaljer kan man ju välja fritt. Men jag tänkte mig en svetsad platta på HEA balken som betongskruv in i infästningen (betong).jonmo skrev:
Min personliga misstanke är att nedböjningen kommer att hamna inom ett hanterbart interval (någon enstaka mm), men att det blir lite krafter i infästningen och för att räkna exakt på detta, dvs. hur resp. skruv skall placeras och dimensioneras så behövs lite mer, men jag tänkte att det kanske blir en senare fråga när man fått fram "grundkrafterna"....?
Produkter som diskuteras: "betongskruv"

Betongskruv
Betongskruvar är robusta skruvar som är speciellt designade för att infästas i betong och andra hårda material. Dessa skruvar är starka och slitstarka, vilket gör dem kapabla att bära tunga belastningar och motstå de krävande
Läs mer
Nedböjningen blir ca 1mm vid 10kN belastning, det dubbla vid dubbla belastningen.
Beräkningen bygger på elementärfall #2 i Karl Björks formelsamling (varje maskiningenjörs bibel)
Dragkraften i ovankant av den röda plåten blir ca 11 / 22 ton beroende på last.
Beräkningen bygger på elementärfall #2 i Karl Björks formelsamling (varje maskiningenjörs bibel)
Dragkraften i ovankant av den röda plåten blir ca 11 / 22 ton beroende på last.
Redigerat:
Lysande! Tack! Jag har inte den boken, men borde kanske köpa om det blir fler fall...G Gabbe1 skrev:
Bara en kontrollfråga; Dragkraft blir alltså närmare 100kN i ö.k. plåt? Antar det gäller fallet för 20kN last? Blir det hälften vid 10kN last?
Ton är väl förvisso inte en kraft… Men hur kan du komma fram till detta utan att ha en bestämd storlek på plåten är ett mysterium för mig?G Gabbe1 skrev:
Det är ju typ en kofot du skissar på och det är ganska grundläggande mekanik att räkna på.
Kraften x hävarmen (längden på HEA) ger vridmoment i infästningen. Sen får du dela vridmomentet med den andra hävarmen (röda plattans längd).
I det här fallet: 20000 x 1300 / 240 (dragkraft i Newton).
Ca 108 kN
Edit: korrigering av tankevurpa.
Kraften x hävarmen (längden på HEA) ger vridmoment i infästningen. Sen får du dela vridmomentet med den andra hävarmen (röda plattans längd).
I det här fallet: 20000 x 1300 / 240 (dragkraft i Newton).
Ca 108 kN
Edit: korrigering av tankevurpa.
Redigerat:
Bästa svaret
Vid närmare eftertanke kan jag just ha gjort en tankevurpa.
Det bör inte bli halva den röda plattans längd utan hela längden.
20000x1300 / 240 = 108 kN dragkraft.
(där fick jag bara för att jag kallade belastningsfallet för grundläggande mekanik)
Det bör inte bli halva den röda plattans längd utan hela längden.
20000x1300 / 240 = 108 kN dragkraft.
(där fick jag bara för att jag kallade belastningsfallet för grundläggande mekanik)
Var också inne på halva längden och förstår faktiskt inte riktigt hur det blir hela?G Gabbe1 skrev:
Du kan välja att göra en momentberäkning kring vilken punkt du vill. Men om beräkningen görs mitt i den röda plåten så tillkommer ju även en tryckkraft i underkant som är lika stor som dragkraften i överkant.S skyisthelimit skrev:
Mest pedagogiskt blir att räkna moment kring röda plåtens nederkant och då kan hela längden tillgodoräknas som hävarm.
Det känns ju som att det behöver vara ordentligt svetsat i plattan framförallt?
Jag antar att alla lösningar med något stag eller vad det kallas är uteslutna? Det hade ju i mitt huvud gjort saken lätt att lösa 😀
Jag hade vågat chansa om jag fick ha två fästpunkter i väggen!
Jag antar att alla lösningar med något stag eller vad det kallas är uteslutna? Det hade ju i mitt huvud gjort saken lätt att lösa 😀
Jag hade vågat chansa om jag fick ha två fästpunkter i väggen!
Ok, då tror jag att jag är med!G Gabbe1 skrev:Du kan välja att göra en momentberäkning kring vilken punkt du vill. Men om beräkningen görs mitt i den röda plåten så tillkommer ju även en tryckkraft i underkant som är lika stor som dragkraften i överkant.
Mest pedagogiskt blir att räkna moment kring röda plåtens nederkant och då kan hela längden tillgodoräknas som hävarm.
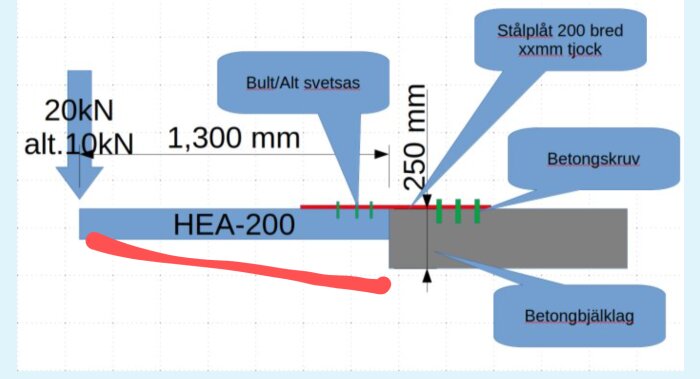
Egentligen handlar "mitt problem" om infästning av en balk i ett bjälklag. Funderade lite till och kom fram till en alternativ lösning som är kanske enklare att praktiskt göra (går att lösa utan svetsning).
Rent belastningsmässigt borde denna lösning då utsätta plåten för ca 137kN om jag räknat rätt (HEA 200 är 190 hög)..... ?
Generella tankar om lösningen (förutom att man kanske bör lägga en plåt bakom HEA:n som fördelar ut lasten lite mot betongen....?
Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder
S skyisthelimit skrev:Ok, då tror jag att jag är med!
Egentligen handlar "mitt problem" om infästning av en balk i ett bjälklag. Funderade lite till och kom fram till en alternativ lösning som är kanske enklare att praktiskt göra (går att lösa utan svetsning).
Rent belastningsmässigt borde denna lösning då utsätta plåten för ca 137kN om jag räknat rätt (HEA 200 är 190 hög)..... ?
Generella tankar om lösningen (förutom att man kanske bör lägga en plåt bakom HEA:n som fördelar ut lasten lite mot betongen....?
[bild]
Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder
?
Naturligtvis är det hela längden från nedre kant till centrum på skruvarna, och det gäller både övre och nedre skruvarna. Jag förstår fortfarande inte hur du kan få fram siffror på det då det inte framgår hur hög den röda plattan är. Den kan ju med fördel vara 500mm lång och med typ 8 skurvar så man kan ju göra vad man vill av det.G Gabbe1 skrev: