Hobbyelektriker
· Värmland, Molkom
· 24 922 inlägg
Din formel närmar sig den tydlighet och enkelhet som jag hade önskat och tror hade behövts i tråden, men saknar förklaringar, främst till 2:an där du genar 
. Det är ju siffran två som du ska räkna fram! Om man nu skulle ha en strömtång och mäter strömmen A med alla faser anslutna och strömmen B med en fas bruten, hur räknar man om denna differens till effekt, både absolut och relativ?
. Det är ju siffran två som du ska räkna fram! Om man nu skulle ha en strömtång och mäter strömmen A med alla faser anslutna och strömmen B med en fas bruten, hur räknar man om denna differens till effekt, både absolut och relativ?
Redigerat:
Med 2 faser:
Effekt i Y
P=(Uh*Uh)/2R
Effekt i D
P=(Uh*Uh)/(1/(1/R)+(1/2R))
Samma effekt i D med ersättningsresistans parallellkopplad som redan nämnts i tråden.
Så effekten blir hälften av den 3fasiga
P=(3*(Uh*Uh))/R
Skillnaden i ström blir en faktor på 0,87 eller 1,15 mellan 2-faser och 3-faser.
(P/√3)/(0,5P)
Effekt i Y
P=(Uh*Uh)/2R
Effekt i D
P=(Uh*Uh)/(1/(1/R)+(1/2R))
Samma effekt i D med ersättningsresistans parallellkopplad som redan nämnts i tråden.
Så effekten blir hälften av den 3fasiga
P=(3*(Uh*Uh))/R
Skillnaden i ström blir en faktor på 0,87 eller 1,15 mellan 2-faser och 3-faser.
(P/√3)/(0,5P)
Hobbyelektriker
· Värmland, Molkom
· 24 922 inlägg
Snyggt. Jag är med på att strömmen förändras med en faktor √3/2 men lite otydligt hur du kom fram till det.
Ja det är väldigt otydligt. Jag satte formlerna för ström med 3 faser och 2 faser på varsin sida om ett likhetstecken där P är effekten med 2-fas och 2P effekten med 3-fas.
I=P/Uh 2-fasigt och I=2P/(√3*Uh) 3-fasigt. Om man kvittar bort allt så blir det ett förhållande på 2/√3 kvar vilket verkade stämma.
Uh=Nominell huvudspänning
P=Uh*I(uppmätt ström B) med en fas bruten.
Vi kompletterar formeln med √3 när vi slår på den brutna fasen och får en trefasig krets.
P=Uh*I(uppmätt ström B)*√3
Vi kompletterar formeln med att multiplicera med 1,15 för att "kompensera" för den sista fasen som kopplas in.
P=Uh*I(uppmätt ström B)*√3*1,15
Uh*I(uppmätt ström B)*√3*1,15 = Uh*I(uppmätt ström A)*√3
Jag tror vi egentligen är ute efter ett enklare sätt att härleda och svara på denna fråga och frågan varför strömmen ändras liknande det GK100 skrev i inlägg 45.
I=P/Uh 2-fasigt och I=2P/(√3*Uh) 3-fasigt. Om man kvittar bort allt så blir det ett förhållande på 2/√3 kvar vilket verkade stämma.
Strömmen A och B bör visa en skillnad där strömmen A är cirka 1.15 gånger större. Ström A/Ström B.
Uh=Nominell huvudspänning
P=Uh*I(uppmätt ström B) med en fas bruten.
Vi kompletterar formeln med √3 när vi slår på den brutna fasen och får en trefasig krets.
P=Uh*I(uppmätt ström B)*√3
Vi kompletterar formeln med att multiplicera med 1,15 för att "kompensera" för den sista fasen som kopplas in.
P=Uh*I(uppmätt ström B)*√3*1,15
Uh*I(uppmätt ström B)*√3*1,15 = Uh*I(uppmätt ström A)*√3
Jag tror vi egentligen är ute efter ett enklare sätt att härleda och svara på denna fråga och frågan varför strömmen ändras liknande det GK100 skrev i inlägg 45.
Jag var väl hyfsat med på matten i skolan men nu känns det trögt att ställa upp formler om man inte måste... så jag gillar den grafiska metoden för att lösa det här problemet.
Rita ut Y och D koppling på ett papper.
Gör man det skalenligt kan man till och med mäta fram spänningarna med tumstock! Kul tex att se hur man flyttar nollpunkten när kretsen inte längre är symetrisk.
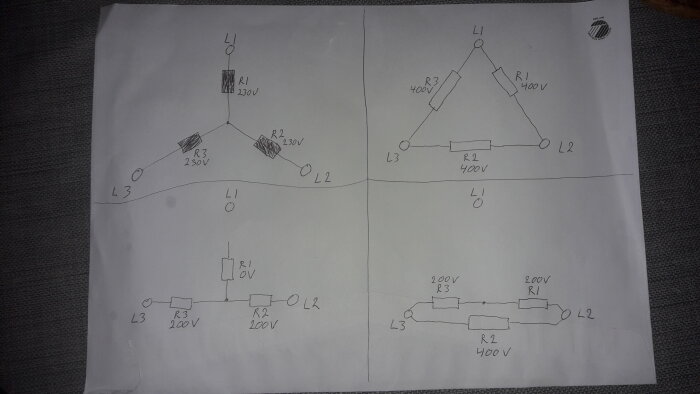
Tänk strecken som gummisnoddar. Varje fas drar i trådarna med en kraft som motsvarar strömstyrkan.
Är strömmarna olika stora så flyttas nollpunkten från mitten.
Släpper man L1 så lägger sig resistanserna rakt mellan L2 och L3. I bilden nere till höger skulle man ritat alla resistanserna uppepå varandra i rak linje.
Det är min lösning.
Rita ut Y och D koppling på ett papper.
Gör man det skalenligt kan man till och med mäta fram spänningarna med tumstock! Kul tex att se hur man flyttar nollpunkten när kretsen inte längre är symetrisk.
Tänk strecken som gummisnoddar. Varje fas drar i trådarna med en kraft som motsvarar strömstyrkan.
Är strömmarna olika stora så flyttas nollpunkten från mitten.
Släpper man L1 så lägger sig resistanserna rakt mellan L2 och L3. I bilden nere till höger skulle man ritat alla resistanserna uppepå varandra i rak linje.
Det är min lösning.
Hobbyelektriker
· Värmland, Molkom
· 24 922 inlägg
Äntligen en skiss som jag väntat på. Åtminstone jag tycker det underlättar med en bild av hur det blir med en fas borta.
För Y-fallet ser man att spänningen ökar med en faktor √3 och resistansen ökar med en faktor 2, alltså √3²/2 = 3/2 = 1.5 tvåpoligt, vilket ska jämföras med trefaseffekten 1*3.
Du har ju sagt att det är bra att förenkla som nämnts flera gånger i tråden, dvs sätta fasspänningen 230 V till 1, huvudspänningen 400 V till √3 och R till 1. Eftersom vi ska jämföra värden så är det bara skillnaden i ingående faktorer av intresse. Dessa förenklingar finns i tabellen nedan.
Gör man det så behöver man ingen miniräknare för att komma fram till förhållandet mellan trefas och en fas borta.
En annan sak man ser i tabellen är förhållandet mellan 230 V och 400 V. R är 1 i båda fallen. Därför ser man effekten 3 för Y-fallet och 9 för D-fallet. Relativt likaså för strömmen.
Det innebär att om man kopplar in en elpatron vars element är avsedda för 230 V till 400 V D-kopplat så ökar effekten med en faktor 3. Detta känner vi igen ifrån VVB'er som kan anslutas antingen till 230 V eller 400 V tvåpoligt.
För Y-fallet ser man att spänningen ökar med en faktor √3 och resistansen ökar med en faktor 2, alltså √3²/2 = 3/2 = 1.5 tvåpoligt, vilket ska jämföras med trefaseffekten 1*3.
Du utgår fortfarande ifrån kunskapen att effekten halveras med en fas borta.A avh67f skrev:
Du har ju sagt att det är bra att förenkla som nämnts flera gånger i tråden, dvs sätta fasspänningen 230 V till 1, huvudspänningen 400 V till √3 och R till 1. Eftersom vi ska jämföra värden så är det bara skillnaden i ingående faktorer av intresse. Dessa förenklingar finns i tabellen nedan.
Gör man det så behöver man ingen miniräknare för att komma fram till förhållandet mellan trefas och en fas borta.
En annan sak man ser i tabellen är förhållandet mellan 230 V och 400 V. R är 1 i båda fallen. Därför ser man effekten 3 för Y-fallet och 9 för D-fallet. Relativt likaså för strömmen.
Det innebär att om man kopplar in en elpatron vars element är avsedda för 230 V till 400 V D-kopplat så ökar effekten med en faktor 3. Detta känner vi igen ifrån VVB'er som kan anslutas antingen till 230 V eller 400 V tvåpoligt.
Rätt så otroligt egentligen att det behövs skisser för att förklara att det är 400V mellan två faser 😉
Hobbyelektriker
· Värmland, Molkom
· 24 922 inlägg
Varför skriver du så? Vad vill du säga? Att "ingen" kan ha så dåliga kunskaper inom ellära? Det matchar nog 98% av befolkningen. Du kom med rätt svar i #3. Sedan drog tråden iväg...snaggletooth skrev:
Försökte vara lite ironisk men det är svårt att nå fram med det...
Men ja, den här tråden spårade ur nästan direkt...
En drygt handfull inlägg hade räckt.
Ja och oberoende hur man väljer göra är upplägget från de som lär ut det som avgör framgången sett till en grupp tex elever. Skulle tro att rätt använt är resonemang kring "bilder" likt ditt förra inlägg en bra början.B Bjober skrev:
Tycker inte det spårade. Ni hade ju en bra diskussion direkt från start man kunde lära sig av. Sedan ställde ju Bo en intressant fråga om strömmen och hur man omsätter skillnaden där till effekten.
Det viktigaste är att trådstartaren får ett svar denna är nöjd med. Oklart om så har skett här.
Det viktigaste är att trådstartaren får ett svar denna är nöjd med. Oklart om så har skett här.
Hobbyelektriker
· Värmland, Molkom
· 24 922 inlägg
Äh, två dygn och ingen har ännu läst mina svammelformler, sorgligt. Hade tänkt bjuda på öl till den förste. Nä, här kommer en bättre version. Men den är väl glömd innan mello ikväll...
Sätt alltså
Sätt alltså
- fasspänningen 230 V till 1,
- huvudspänningen 400 V till √3 och
- R till 1.
