För att lära mig mer om det här med nedböjning och hållfasthetsberäkningar tänkte jag be om hjälp med ett räkneexempel.
Förutsättningar:
Carport L8000xB6000 mm
Höjd betongplatta till takstol 2500 mm
Limträpelare 115x115 mm
4st 45x120 skruvlimmade C24 reglar i punkt B
Limträbalk 115x315x6000 mm
Tungt yttertak (betongpannor, råspont)
Taket sticker ut 300 mm utanför takstolarna
Lätt innertak (råspont)
Takstolar fribärande W, 6000 mm breda, 27 graders lutning
EDIT: Tar med dessa värden för att ha nått att räkna ifrån:
Snözon: 2,5 kN/m2
Egentyngd yttertak: 0,9 kN/m2
Egentyngd innertak: 0,25 kN/m2
Detta ger taklast 3,65 kN/m2
Takstolarna sitter cc 1200 mm, men pga carporten är 8000 mm lång så blir det kortare cc mellan två av dem. Balken är inskjuten i förrådsdelen ca 400 mm. Min fundering är nu vart takstolen längst till vänster på balken ska sitta, i punkt A eller punkt B:
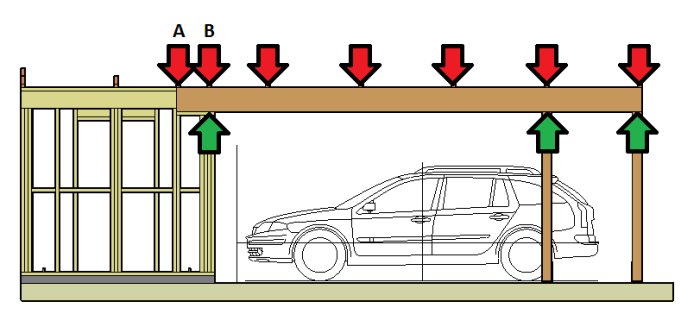
Hur mycket minskas nedböjningen på balken om jag väljer punkt A? Och hur räknar jag ut nedböjningen?
Förutsättningar:
Carport L8000xB6000 mm
Höjd betongplatta till takstol 2500 mm
Limträpelare 115x115 mm
4st 45x120 skruvlimmade C24 reglar i punkt B
Limträbalk 115x315x6000 mm
Tungt yttertak (betongpannor, råspont)
Taket sticker ut 300 mm utanför takstolarna
Lätt innertak (råspont)
Takstolar fribärande W, 6000 mm breda, 27 graders lutning
EDIT: Tar med dessa värden för att ha nått att räkna ifrån:
Snözon: 2,5 kN/m2
Egentyngd yttertak: 0,9 kN/m2
Egentyngd innertak: 0,25 kN/m2
Detta ger taklast 3,65 kN/m2
Takstolarna sitter cc 1200 mm, men pga carporten är 8000 mm lång så blir det kortare cc mellan två av dem. Balken är inskjuten i förrådsdelen ca 400 mm. Min fundering är nu vart takstolen längst till vänster på balken ska sitta, i punkt A eller punkt B:

Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder
Hur mycket minskas nedböjningen på balken om jag väljer punkt A? Och hur räknar jag ut nedböjningen?
Redigerat:
Medlem
· Blekinge
· 10 117 inlägg
Det är bara de tre takstolslaster som hamnar på limträbalkens största spann som påverkar nedböjningen. Övriga takstolar hamnar över en pelare (oberoende av om du väljer A eller B) och orsakar därför ingen böjning i balken. Formeln för att beräkna nedböjningen på en fritt upplagd balk är 5qL^4/384EI. q = utbredd last, L= spännvidd, E=elasticitetsmodul och I=yttröghetsmoment. Det gäller att använda rätt enhet på de olika faktorerna för att få ett begripligt resultat.
Ok, vi börjar med att beräkna nedböjningen för den stora öppningen som sätts till 4300 mm.
q, utbredd last: 3,65 kN/m2 har vi. Total bredd på takstolarna är 7 meter vilket ger en last per meter på 7x3,65=25,55 kN/m. Upplagets längd är 4,3 meter vilket ger 4,3x25,55=109,865 ~110 kN för hela taket. Vi delar detta på två då det ju finns två sidor. 110/2=55 kN.
L, spännvidd antar jag är 4300 mm (vilken enhet ska det vara?)
E, elasticitetsmodul är knepigare för en novis, men jag hittade en tabell från Moeven (limträhandboken) där jag fann att en GL30c balk har en karakteristisk elasticitetsmodul på 10800 N/mm2. Fanns även parallellt/vinkelrätt fibrerna, är det karakteristisk vi ska använda?
I, yttröghetsmoment hittar jag inte! Såg en formel i nån tråd här på forumet, men kunde inte tyda vad det var för siffror i den.
q= 55 kN
L= 4300 mm
E= 10800 N/mm2
I= ?
q, utbredd last: 3,65 kN/m2 har vi. Total bredd på takstolarna är 7 meter vilket ger en last per meter på 7x3,65=25,55 kN/m. Upplagets längd är 4,3 meter vilket ger 4,3x25,55=109,865 ~110 kN för hela taket. Vi delar detta på två då det ju finns två sidor. 110/2=55 kN.
L, spännvidd antar jag är 4300 mm (vilken enhet ska det vara?)
E, elasticitetsmodul är knepigare för en novis, men jag hittade en tabell från Moeven (limträhandboken) där jag fann att en GL30c balk har en karakteristisk elasticitetsmodul på 10800 N/mm2. Fanns även parallellt/vinkelrätt fibrerna, är det karakteristisk vi ska använda?
I, yttröghetsmoment hittar jag inte! Såg en formel i nån tråd här på forumet, men kunde inte tyda vad det var för siffror i den.
q= 55 kN
L= 4300 mm
E= 10800 N/mm2
I= ?
Ok! Jag köper att det så klart påverkar var på balken lasterna kommer. Och då kommer så klart följdfrågan hur jag får in det i formeln?R felixmartensson skrev:
När vi ändå är inne på laster, ska jag addera något för vindlast? Alltså när taket agerar segel där vinden trycker ner taket mot marken?
Medlem
· Blekinge
· 10 117 inlägg
Balkens yttröghetsmoment beräknas enligt formeln b*h^3/12. En 115x315 balk har således ett yttröghetsmoment på 29954 cm4. Snölast räknas alltid i horisontalplanet. En 6 m bred takstol på c/c 1200 mm utsätts då för en snölast på 6*1,2*2,5 = 18 kN, varav 9 kN hamnar på ett upplag. Jag bortser från ev formfaktorer. Takets egenvikt på en takstol blir 8*1,2'1,15 = 11,04 kN, dvs 5,52 kN per upplag. Varje takstol representerar alltså en punktlast på 9 + 5,52 = 14,52 kN. 14,52/1,2 m = 12,1/m. Sätter man in dessa värden i formeln 5qL^4/384EI med rätt enheter blir resultatet 16,7 mm.
Tack Justus! Jag repeterar för min egen skull (och för andra som kanske läser):J justusandersson skrev:Balkens yttröghetsmoment beräknas enligt formeln b*h^3/12. En 115x315 balk har således ett yttröghetsmoment på 29954 cm4. Snölast räknas alltid i horisontalplanet. En 6 m bred takstol på c/c 1200 mm utsätts då för en snölast på 6*1,2*2,5 = 18 kN, varav 9 kN hamnar på ett upplag. Jag bortser från ev formfaktorer. Takets egenvikt på en takstol blir 8*1,2'1,15 = 11,04 kN, dvs 5,52 kN per upplag. Varje takstol representerar alltså en punktlast på 9 + 5,52 = 14,52 kN. 14,52/1,2 m = 12,1/m. Sätter man in dessa värden i formeln 5qL^4/384EI med rätt enheter blir resultatet 16,7 mm.
I=b*(h^3)/12
b=11,5 cm
h=31,5 cm
I=11,5*(31,5^3)/12
I=29953,546875 cm4
I=29954 cm4
Bifogar bild på takstolen i fråga:
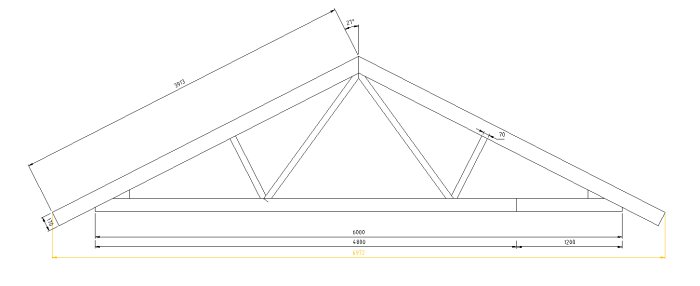
Visst borde takets bredd vara 7 meter när vi räknar på snölasten?
Dvs. 7*2,5=17,5 kN/m vilket ger 17,5*1,2/2=10,5 kN punktlast per upplag?
Och då kommer ytterligare en fråga om takets egentyngd per meter; ska den i detta fall räknas (3,9+3,9)*0,9+(3,9+3,9)*0,25=7,02+1,95=8,97 kN/m för hela taket? Dvs att man tar hänsyn till vinkeln på takstolen och tar hela överliggarens längd?
Punktlast egentyngd tak per upplag blir då 8,97*1,2/2=5,382 kN
Punktlast på varje upplag blir 10,5+5,382=15,882 kN
Om q utbredd last ska vara i kN/m så räknar vi tillbaka igen: 15,882/1,2=13,235 kN/m
Kan jag få hjälp med rätt enheter till 5qL^4/384EI?
q= 13235 N/m
L= 4,3 m
E= 10800000 N/m2
I= 299,54 m4
Medlem
· Blekinge
· 10 117 inlägg
Absolut, fast det har inte framgått av tidigare redovisning. För takets egenvikt räknar man givetvis på hela takytan. Om du använder enheterna N/m, m, N/m2 och m4 kommer du att få ett resultat i meter. Rätt många decimaler alltså. Man kan använda vilka enheter man vill bara man gör det konsekvent. Ett tips: Uträkningen blir mycket enklare att felsöka om du lägger in den på ett Excel-ark. Dessutom kan du ändra parametrarna för att testa konsekvenserna.murak skrev:
Att konvertera enheter var för mig en utmaning, men nu har jag lyckats (tror jag). Jag gjorde allt till meter:
q= 13235 N/m
L= 4,3 m
E= 10800000000 N/m2
I= 0,00029954 m4
Vilket ger mig en nedböjning på 0,0182 meter, dvs 18,2 mm.
Detta ger L/236 vilket väl inte är önskvärt? Jag har bett Martinsons Byggsystem räkna på balken och jag fick deras beräkningsresultat på mail. Där får dom följande deformationer:
Abs. - total last: -13 mm
Abs. variabel last: -9 mm
Dom har troligen inte samma ingångsvärden som jag tagit här ovan, så nu vill jag kika på takets egenvikt.
Kanske är 0,9 kN/m2 för högt räknat för mitt yttertak? Vi går igenom det:
Betongpannor: Benders Palema
Ströläkt/bärläkt: 25x36 gran, ströläkt på cc600mm, bärläkt på cc356mm
Takpapp: Mataki MB320 vikt 2 kg/m2
Råspont: 20x120 gran
Jag får leta efter vikt/m2 på respektive post, men om någon har det i huvudet så fyll gärna på.
q= 13235 N/m
L= 4,3 m
E= 10800000000 N/m2
I= 0,00029954 m4
Vilket ger mig en nedböjning på 0,0182 meter, dvs 18,2 mm.
Detta ger L/236 vilket väl inte är önskvärt? Jag har bett Martinsons Byggsystem räkna på balken och jag fick deras beräkningsresultat på mail. Där får dom följande deformationer:
Abs. - total last: -13 mm
Abs. variabel last: -9 mm
Dom har troligen inte samma ingångsvärden som jag tagit här ovan, så nu vill jag kika på takets egenvikt.
Kanske är 0,9 kN/m2 för högt räknat för mitt yttertak? Vi går igenom det:
Betongpannor: Benders Palema
Ströläkt/bärläkt: 25x36 gran, ströläkt på cc600mm, bärläkt på cc356mm
Takpapp: Mataki MB320 vikt 2 kg/m2
Råspont: 20x120 gran
Jag får leta efter vikt/m2 på respektive post, men om någon har det i huvudet så fyll gärna på.
Betongpannor: Benders Palema Torrvikt: 36 kg/m2
Ströläkt/bärläkt: 25x36 gran, ströläkt på cc600mm, bärläkt på cc356mm Orkar inte leta mer, men hittade en schablon på 5 kg/m2
Takpapp: Mataki MB320 Torrvikt: 2 kg/m2
Råspont: 20x120 gran Torrvikt: 9,51 kg/m2
Detta ger: 52,5 kg/m2 vilket blir ungefär 0,53 kN/m2.
Och då kommer frågan vad jag ska addera för takstolarna, dom väger ju en del dom med..
Ströläkt/bärläkt: 25x36 gran, ströläkt på cc600mm, bärläkt på cc356mm Orkar inte leta mer, men hittade en schablon på 5 kg/m2
Takpapp: Mataki MB320 Torrvikt: 2 kg/m2
Råspont: 20x120 gran Torrvikt: 9,51 kg/m2
Detta ger: 52,5 kg/m2 vilket blir ungefär 0,53 kN/m2.
Och då kommer frågan vad jag ska addera för takstolarna, dom väger ju en del dom med..
Medlem
· Blekinge
· 10 117 inlägg
Torrt trä (fur eller gran) har en volymvikt på 0,5 kg/dm3. Det betyder att en 1 m lång 45x145 regel väger 3,26 kg.
Utmärkt, då ska vi se..
0,045*0,170*7,8=0,05967m3
0,045*0,145*6=0,03915m3
0,045*0,07*5,15=0,0162225m3
=0,115m3 per takstol. 0,115*500=57,5kg/stol
Spikplåtar... Ursäkta att jag inte skriver storlek, om någon undrar så tar jag det då.
4*0,89kg=3,56kg
2*0,56kg=1,12kg
6*0,3kg=1,8kg
4*0,143kg=0,572kg
=7,052kg/stol
Ankarskruv..
Vikt 1 kg/250st ger 0,004kg/st. Grovt räknat 200 skruv/stol ger 200*0,004=0,8kg/stol
Totalvikt: 57,5+7,052+0,8=65,352 kg/stol eller 0,640884 kN/stol
*Puh..
Jag skrev tidigare att egenvikten för själva yttertaket blev 52,5 kg/m2 vilket mer exakt blir 0,514849 kN/m2
Om vi nu ska försöka slå ihop allt detta i kN/m för vår/min balk så får vi:
Yttertak 0,514849*7,8/2=4,0158/2=2,0079~ 2 kN/m
Takstolar 0,640884/1,2=0,53407~ 0,53 kN/m
Snölasten 10,5/1,2= 8,75 kN/m
(Jag tar bort innertaket i detta skede!)
2+0,53+8,75= 11,28 kN/m
In med det i formeln så får jag 15,5 mm nedböjning eller L/277 :/
0,045*0,170*7,8=0,05967m3
0,045*0,145*6=0,03915m3
0,045*0,07*5,15=0,0162225m3
=0,115m3 per takstol. 0,115*500=57,5kg/stol
Spikplåtar... Ursäkta att jag inte skriver storlek, om någon undrar så tar jag det då.
4*0,89kg=3,56kg
2*0,56kg=1,12kg
6*0,3kg=1,8kg
4*0,143kg=0,572kg
=7,052kg/stol
Ankarskruv..
Vikt 1 kg/250st ger 0,004kg/st. Grovt räknat 200 skruv/stol ger 200*0,004=0,8kg/stol
Totalvikt: 57,5+7,052+0,8=65,352 kg/stol eller 0,640884 kN/stol
*Puh..
Jag skrev tidigare att egenvikten för själva yttertaket blev 52,5 kg/m2 vilket mer exakt blir 0,514849 kN/m2
Om vi nu ska försöka slå ihop allt detta i kN/m för vår/min balk så får vi:
Yttertak 0,514849*7,8/2=4,0158/2=2,0079~ 2 kN/m
Takstolar 0,640884/1,2=0,53407~ 0,53 kN/m
Snölasten 10,5/1,2= 8,75 kN/m
(Jag tar bort innertaket i detta skede!)
2+0,53+8,75= 11,28 kN/m
In med det i formeln så får jag 15,5 mm nedböjning eller L/277 :/
Produkter som diskuteras: "Ankarskruv"

Ankarskruv
Ankarskruvar är speciella skruvar som används främst för att fästa och förankra byggbeslag och andra konstruktionskomponenter. Dessa skruvar är kända för deras styrka och stabilitet.
Läs mer
Jag redigerar lite..
Det är tre takstolar som verkar på balken vilket ger totalvikt för dessa:
0,640884*3=1,922652 kN
Sen ska jag dela detta på två då det är två balkar som bär upp det hela:
1,922652/2=0,961326 kN
Jag delar med balkens längd för att få kN/m:
0,961326/4,3=0,22356~0,22 kN/m
Detta ger:
Yttertak: 2 kN/m
Takstolar: 0,22 kN/m
Snölast: 8,75 kN/m
2+0,22+8,75=10,97 kN/m (10970 N/m)
Detta ger (med hjälp av min fina excel-snurra, tack för tipset!) en nedböjning på 15,09 mm och L/284,86
Är E= 10800000000 N/m2 och I= 0,00029954 m4 korrekta eller finns det nått där som ska kollas upp?
Att göra den fria öppningen mindre gör att nedböjningen snabbt också blir mindre. Minskar jag till 4 meter öppning så blir nedböjningen 11,3 mm och L/353,88.
Ursprunget till tråden var att bestämma vart takstolen längst till vänster på balken bör placeras för att minska nedböjningen mest. Det kommer ju bli ett moment kring pelare 1 och 2 i bilden nedan som kommer motverka nedböjningen.
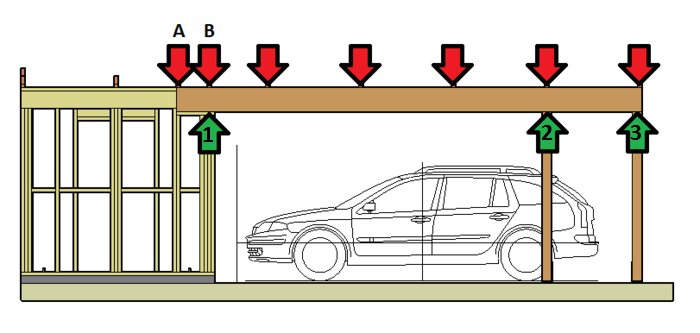
Frågan är hur mycket det påverkar... Resultatet 15,09 mm är ju på en fritt upplagd balk utan hjälpande moment.
Det är tre takstolar som verkar på balken vilket ger totalvikt för dessa:
0,640884*3=1,922652 kN
Sen ska jag dela detta på två då det är två balkar som bär upp det hela:
1,922652/2=0,961326 kN
Jag delar med balkens längd för att få kN/m:
0,961326/4,3=0,22356~0,22 kN/m
Detta ger:
Yttertak: 2 kN/m
Takstolar: 0,22 kN/m
Snölast: 8,75 kN/m
2+0,22+8,75=10,97 kN/m (10970 N/m)
Detta ger (med hjälp av min fina excel-snurra, tack för tipset!) en nedböjning på 15,09 mm och L/284,86
Är E= 10800000000 N/m2 och I= 0,00029954 m4 korrekta eller finns det nått där som ska kollas upp?
Att göra den fria öppningen mindre gör att nedböjningen snabbt också blir mindre. Minskar jag till 4 meter öppning så blir nedböjningen 11,3 mm och L/353,88.
Ursprunget till tråden var att bestämma vart takstolen längst till vänster på balken bör placeras för att minska nedböjningen mest. Det kommer ju bli ett moment kring pelare 1 och 2 i bilden nedan som kommer motverka nedböjningen.

Inloggade ser högupplösta bilder
Logga in
Skapa konto
Gratis och tar endast 30 sekunder
Frågan är hur mycket det påverkar... Resultatet 15,09 mm är ju på en fritt upplagd balk utan hjälpande moment.
Medlem
· Blekinge
· 10 117 inlägg
I= 0,00029954 kan inte ändras med mindre än att balkens dimensioner ändras. Elasticitetsmodulen har lite olika värden beroende på sammanhanget. För deformationsberäkningar har GL 30c normalt E-modulen 13000 MPa. Det är dock inte fel att räkna lite lågt. Hade du haft en utbredd last mellan pelare 2 och 3 så hade den gett upphov till ett negativt moment över pelare 2 som hade motverkat nedböjningen. Nu har du inte det eftersom takstolarna landar rakt över pelarna.