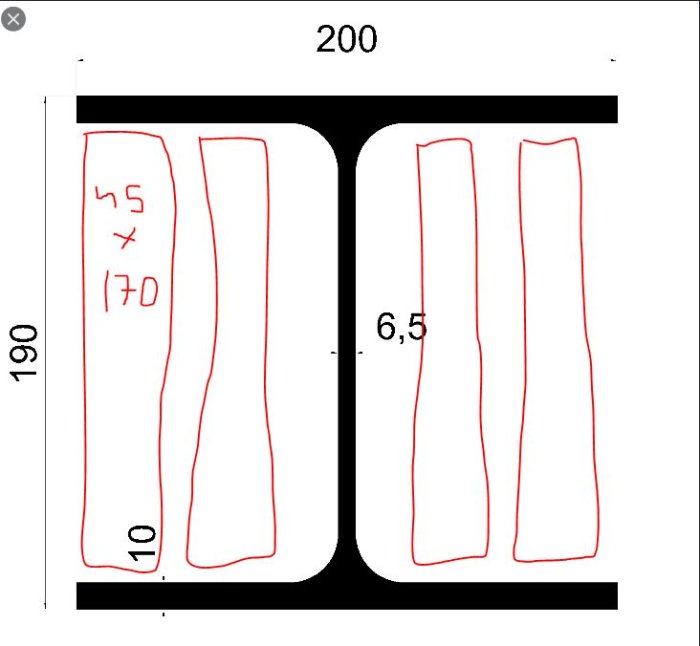
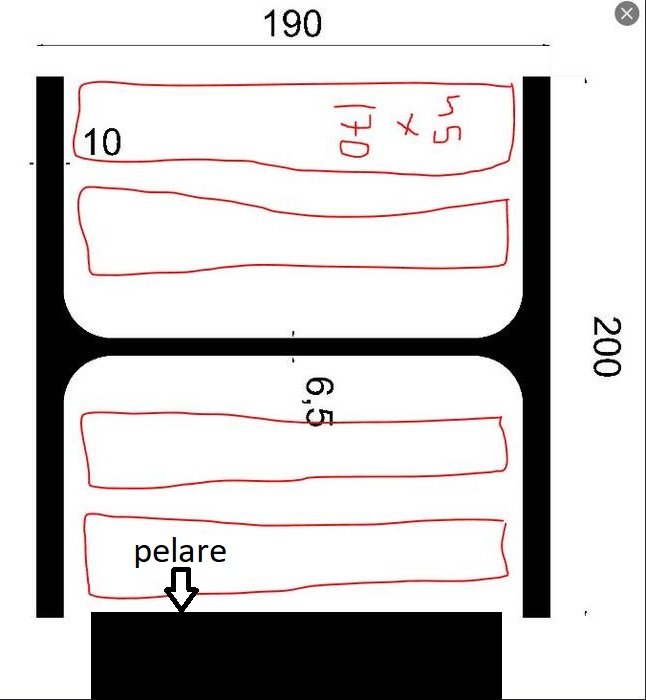
Fyllning med trä ger i stort sett ingenting i styvhet. Vid samma deformation kommer i stort sett all last att tas upp av stålbalken, som materialmässigt har ca 40 ggr större styvhet än trä. Som tankeexperiment: lägg en gummisnodd på en stållinjal och utsätt sandwichen för dragpåkänning. Vilket material tar huvuddelen av lasten?
Om du överhuvudtaget skall få någon hjälp av träreglarna så måste de samverka med stålbalken, dvs vara "kopplade" till varandra och inte bara "inkilade". Nu skiljer det väldigt mycket mellan hållfastheterna mellan stål och trä så det eventuella tillskottet här är nog att betrakta som försumbart.
Hur menar du med kopplade?R roli skrev:
tja man kan ju leka med tanken att det blir styvare MEN när balken brister är det en sån kraft så att det inte spelar någon roll vad det är för dimension elr antal brädbitar emellan .... MEN är ju nu spekulerat på värsta tänka bara scenario att det klipps av på en gång ^^
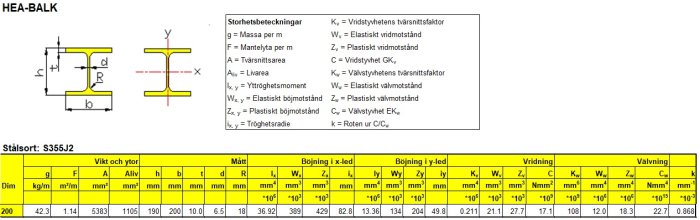
men min teori i min lilla rosa värld att man måst räkna hålfastheten skilt för sig för balken (HEA från storleken) och trä(C16 C24 C30) och sen är spännvid och belastning som vill vara med och leka ... så kan man var nitisk med infästning av trävirket... använding av bultpistol hur mycket påverkar hålen i balken etc
finns mycket
men min teori i min lilla rosa värld att man måst räkna hålfastheten skilt för sig för balken (HEA från storleken) och trä(C16 C24 C30) och sen är spännvid och belastning som vill vara med och leka ... så kan man var nitisk med infästning av trävirket... använding av bultpistol hur mycket påverkar hålen i balken etc
finns mycket
Nej. Ni tänker fel. Infästningen av materialen i varandra har en försumbar betydelse i det här fallet. Skulle det vara en sandwichkonstruktion så är det viktigt, men så är det inte.
Nedböjningen för en given geometri är direkt proportionell mot materialets E-modul. E-modulen är en materialkonstant för ett materials styvhet. Stål har ca 210 GPa och trä någonstans kring 5 GPa. Det är en skillnad på en faktor 40. Nu har visserligen de olika materialen olika geometrier, men det har liten betydelse för resonemanget. Om vi sätter ihop trä med stål enligt den första skissen, så kommer belastningen att ge exakt samma deformation, eller hur? De sitter ju ihop. Spänningen i en belastad konstruktion med en given deformation är direkt beroende av E-modulen. Detta kallas Hookes lag. Det leder till att spännigen i stålet blir så mycket högre att det tar i stort sett hela lasten, och trät tar nästan ingen last alls. Med så låg spänning i trät kommer styvheten i den totala konstruktionen knappt påverkas alls av att man lägger in trä.
Nedböjningen för en given geometri är direkt proportionell mot materialets E-modul. E-modulen är en materialkonstant för ett materials styvhet. Stål har ca 210 GPa och trä någonstans kring 5 GPa. Det är en skillnad på en faktor 40. Nu har visserligen de olika materialen olika geometrier, men det har liten betydelse för resonemanget. Om vi sätter ihop trä med stål enligt den första skissen, så kommer belastningen att ge exakt samma deformation, eller hur? De sitter ju ihop. Spänningen i en belastad konstruktion med en given deformation är direkt beroende av E-modulen. Detta kallas Hookes lag. Det leder till att spännigen i stålet blir så mycket högre att det tar i stort sett hela lasten, och trät tar nästan ingen last alls. Med så låg spänning i trät kommer styvheten i den totala konstruktionen knappt påverkas alls av att man lägger in trä.
Redigerat:
Klicka här för att svara