I praktiken så påverkar förstås ett hyllplan 1000m upp väldigt mycket mera, men det beror ju på att det är helt omöjligt att få det 100% styvt.A ArneTW skrev:
De högre hyllplanen påverkar ju också mera om hyllan belastas för mycket så övre skruven dras ut lite från väggen. Ju mer den dras ut, ju mera påverkar det hur högt upp man lagt tunga saker.
Hobbyelektriker
· Värmland, Molkom
· 25 221 inlägg
Tack cpalm.
Jag försökte räkna på kraftkomposanter.
Ytterlighetsfallen är enkla, även om jag inte kan förklara med ord varför det översta hyllplanet orsakar samma utdragande kraft på övre skruven som det understa hyllplanet.
Det mellersta ger ett tryck på nedre skruven och drag på övre skruven.
Jag har dock fastnat på hur krafterna fördelas för ett hyllplan som sitter på 1/4 av höjden. Jag tänker mig att fördelningen är förhållandet mellan vinklarna eller längden på hypotenusan?
Jag försökte räkna på kraftkomposanter.
Ytterlighetsfallen är enkla, även om jag inte kan förklara med ord varför det översta hyllplanet orsakar samma utdragande kraft på övre skruven som det understa hyllplanet.
Det mellersta ger ett tryck på nedre skruven och drag på övre skruven.
Jag har dock fastnat på hur krafterna fördelas för ett hyllplan som sitter på 1/4 av höjden. Jag tänker mig att fördelningen är förhållandet mellan vinklarna eller längden på hypotenusan?
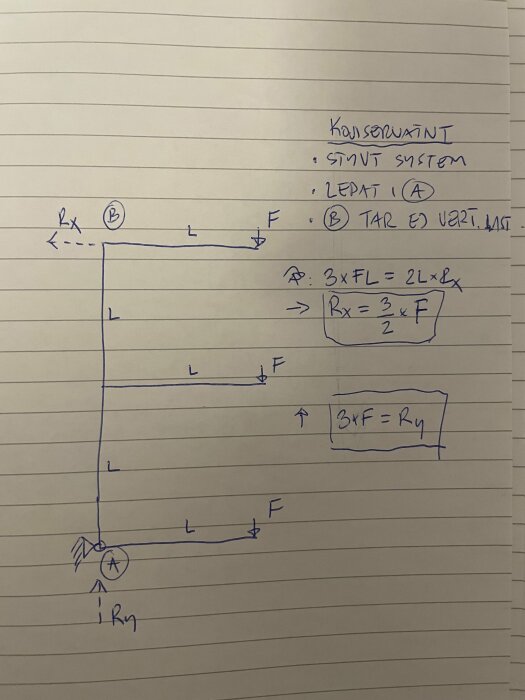
Känns som att ni krånglar till det lite… Gör en konservativ uppställning och anta att 1) allt är oändligt styvt samt 2) att hyllan är ledad i A samt att alla vertikala laster tas upp i A och 3) att alla horisontella reaktionskrafter tas upp i B samt 4) att L respektive F i skissen gäller
Nu har vi maximala belastningen och den är definitivt konservativ eftersom ingenting är styvt i verkligheten samt att de vertikala lasterna fördelas mellan skruvarna i A respektive B
Nu har vi maximala belastningen och den är definitivt konservativ eftersom ingenting är styvt i verkligheten samt att de vertikala lasterna fördelas mellan skruvarna i A respektive B
Ja, för att förtydliga var min avsikt att förklara TS "omväg" med de imaginära hävstängerna. När man väl insett att man inte behöver tänka så blir lösningen trivial.J Jo-han skrev:
Hobbyelektriker
· Värmland, Molkom
· 25 221 inlägg
Jo med detta antagande spelar det ingen roll var hyllplanen finns. Man behöver bara summera dem. Men om man nu inte har några sidoväggar och har ett hyllplan på 3/8 höjd?
J Jo-han skrev:
Är inte helt säker på att jag förstår vad du menar men det låter som ett statiskt obestämt system, dvs det går inte att räkna ut det med jämviktsekvationerna. Men som sagt, kan vara så att jag helt missförstår…
Hobbyelektriker
· Värmland, Molkom
· 25 221 inlägg
Jag tänker nånting sånt här. Tydligen ska dessa hyllor klara 200 kg.
Bilder är bra 😅 Och vad är det du vill räkna ut?
Det som påverkar är när skenan böjs och ger ett tryck på väggen högre upp än längst ner. Det är givetvis inte det enda som spelar roll. Om väggen är ojämn eller böjlig påverkas också resultatet. Om man pallar under skenan i underkant med en liten kloss så att den inte nuddar väggen mellan övre och undre fästpunkt så kompenserar man för utböjningen och resultatet stämmer bra. Man kan säkert ta fram en formel som tar hänsyn till väggens och skenans styvhet så att man får fram den dragande kraften på skruven. Men om väggen inte är plan eller om det finns reglar bakom gipsskivan så blir det ännu bökigare. Antagandet i första inlägget att väggen och skenan är styva ger ett rimligt värde. Jag tror att de flesta sätter upp sina hyllor utan att göra beräkningar med finita element-metoden. Och det är lite över nivån på en sådan här skoluppgift också.
Hobbyelektriker
· Värmland, Molkom
· 25 221 inlägg
Tack, jag visade visserligen en bild på en riktig hylla men jag tänker fortfarande på TS grundfråga, hur man beräknar utdragningskraften på skruven längst upp fast med kraftkomposanter istället för vridmoment. Detta med de antaganden som gjorts om ett styvt system etc. Jag har svårt att förstå/räkna hur krafterna fördelas för ett hyllplan på godtycklig höjd som är infäst uppe o nere. Kanske spelar snedsträvor/hyllsidor ingen roll när det är styvt? Det är alltså inget praktiskt problem jag försöker lösa utan jag ville bara lära mig.
Det
I vissa system kan du inte ställa upp en entydig kraftjämvikt (kraftens fördelning är alltså inte entydigt bestämd) och du får två eller flera okända resulterande krafter, dvs. ett statiskt obestämt system. Det är inte ofördelaktigt i praktiken för det ger ofta en god redundans i ett system om något stag tex. skulle haverera.
Ett skruvförband tar upp antingen drag- eller skjuvkrafter eller vanligtvis en kombination av båda. I en hylla, som i detta exemplel, är det nog omöjligt att i praktiken dra skruven med tillräckligt moment för att klämkraften mellan väggen och skenan ska bli tillräckligt stor så friktionskraften däremellan överstiger egentyngden av hyllan, dvs så skruven inte behöver ta den skjuvlasten. Därav det konservativa angreppssättet att säga att endast en av skruvarna tar all skjuvlast, medan i verkligheten så fördelas den nog ganska jämnt mellan övre och undre skruven i exemplet.
När det gäller dragkraften i den övre skruven så spelar det ingen roll på vilken höjd i hyllan du lägger dina 200kg utan det som avgör är hur långt ut från väggen som lasten är placerad.
Man skulle kunna tänka sig att den 2-dimensionella hyllan jag ritade i skissen står på ett hårt underlag och balanserar. Eftersom hyllplanen bidrar med viss massa så kommer den inte att stå upprätt av sig självt utan du behöver hålla fast den i sidled. Lägger du på 200kg så behöver du hålla hårdare och skulle du flytta dina 200kg mellan hyllplanen så blir det ingen skillnad.
Slutsatsen är att flyttar du skruven nedåt (och behåller hyllplan och last på samma ställe) så kommer dragkraften i skruven att öka medan om du flyttar den uppåt så kommer den således minska men det spelar fortfarande ingen roll var i hyllan du har lagt sina 200kg.
Det intressanta blir resonemanget kring när du ska fästa varje skena med 3 skruvar; där en sätts lägst upp och en längst ner, men var sätter du den tredje och varför?! Blir det statiskt bestämt med en tredje skruv? Dvs, kan du räkna ut hur lasten mellan dem fördelas?
Det där med moment kring en viss punkt är lite lurigt, för det vi är ute efter är kraftjämvikter runt den punkten som beräknas för att kunna lösa ut den okända resulterande kraften. Vi är inte intresserade av något moment i detta fallet.
I vissa system kan du inte ställa upp en entydig kraftjämvikt (kraftens fördelning är alltså inte entydigt bestämd) och du får två eller flera okända resulterande krafter, dvs. ett statiskt obestämt system. Det är inte ofördelaktigt i praktiken för det ger ofta en god redundans i ett system om något stag tex. skulle haverera.
Ett skruvförband tar upp antingen drag- eller skjuvkrafter eller vanligtvis en kombination av båda. I en hylla, som i detta exemplel, är det nog omöjligt att i praktiken dra skruven med tillräckligt moment för att klämkraften mellan väggen och skenan ska bli tillräckligt stor så friktionskraften däremellan överstiger egentyngden av hyllan, dvs så skruven inte behöver ta den skjuvlasten. Därav det konservativa angreppssättet att säga att endast en av skruvarna tar all skjuvlast, medan i verkligheten så fördelas den nog ganska jämnt mellan övre och undre skruven i exemplet.
När det gäller dragkraften i den övre skruven så spelar det ingen roll på vilken höjd i hyllan du lägger dina 200kg utan det som avgör är hur långt ut från väggen som lasten är placerad.
Man skulle kunna tänka sig att den 2-dimensionella hyllan jag ritade i skissen står på ett hårt underlag och balanserar. Eftersom hyllplanen bidrar med viss massa så kommer den inte att stå upprätt av sig självt utan du behöver hålla fast den i sidled. Lägger du på 200kg så behöver du hålla hårdare och skulle du flytta dina 200kg mellan hyllplanen så blir det ingen skillnad.
Slutsatsen är att flyttar du skruven nedåt (och behåller hyllplan och last på samma ställe) så kommer dragkraften i skruven att öka medan om du flyttar den uppåt så kommer den således minska men det spelar fortfarande ingen roll var i hyllan du har lagt sina 200kg.
Det intressanta blir resonemanget kring när du ska fästa varje skena med 3 skruvar; där en sätts lägst upp och en längst ner, men var sätter du den tredje och varför?! Blir det statiskt bestämt med en tredje skruv? Dvs, kan du räkna ut hur lasten mellan dem fördelas?