Dimensionering stödbalk låglutande tak.
Hej!
Har ett garage med låglutande tak uppskattar det till mindre än 3°.
Det har en spännvidd på 5,8m invändigt i "två fack".
Stödet i mitten är en inklädd balk med två pelare.
Balkens spännvidd är 5,7m invändigt med pelarna 1,9m från ytterväggarna.
Balken plus inklädnad är ca 160x160mm så gissar på att det är en 145x145 eller 3st 45x145mm(tar givetvis reda på detta innan jag gör något skarpt i detta projekt).
Pelarna är 95x120mm och är 2.05m höga.
Garaget är i snözon 3, men jag vill gärna ta höjd för 3,5.
De befintliga pelarna i garaget är OTROLIGT mycket i vägen och jag vill ha "bort" dem.
Så tänker mig att jag flyttar ut dem mot ytterväggarna och sätter en bättre balk.
Jag antar att takets egentyngd är 0,5kN/m²(mer troligt kring 0,3 i verkligheten) och snölasten är 3,5kN/m².
Således totalt 4kN/m².
Jag utgår från att taket är 6x6m dvs 36m².
Den totala tyngden på taket är då 144kN.
Partialkoefficient 1,25
Säkerhetsklass 2 = 0,91
Klimatklass 0
Typ så långt kommer jag, kan någon hjälpa mig vidare?
Egentligen vill jag inte att att balken kommer ner mer än kanske ca 250mm från taket då det redan nu endast är 205cm under befintlig balk.
Pelarna tänkte jag typ 3st 45x145 i varje ände.
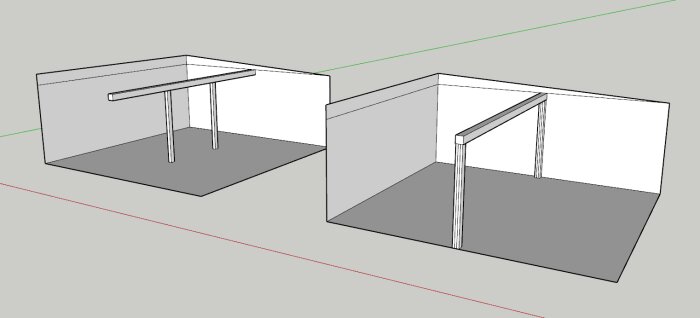
Bifogar bild på hur jag har det idag till vänster och hur jag skulle vilja ha det till höger.
EDIT: I dagsläget skottar jag taket 1-2ggr per vinter inte för att det behövs men för att det känns bra och hade tänkt fortsätta med det men vill inte heller lämna ett tvång till någon annan om jag skulle gå och dö eller om jag skulle bli sjuk.
Har ett garage med låglutande tak uppskattar det till mindre än 3°.
Det har en spännvidd på 5,8m invändigt i "två fack".
Stödet i mitten är en inklädd balk med två pelare.
Balkens spännvidd är 5,7m invändigt med pelarna 1,9m från ytterväggarna.
Balken plus inklädnad är ca 160x160mm så gissar på att det är en 145x145 eller 3st 45x145mm(tar givetvis reda på detta innan jag gör något skarpt i detta projekt).
Pelarna är 95x120mm och är 2.05m höga.
Garaget är i snözon 3, men jag vill gärna ta höjd för 3,5.
De befintliga pelarna i garaget är OTROLIGT mycket i vägen och jag vill ha "bort" dem.
Så tänker mig att jag flyttar ut dem mot ytterväggarna och sätter en bättre balk.
Jag antar att takets egentyngd är 0,5kN/m²(mer troligt kring 0,3 i verkligheten) och snölasten är 3,5kN/m².
Således totalt 4kN/m².
Jag utgår från att taket är 6x6m dvs 36m².
Den totala tyngden på taket är då 144kN.
Partialkoefficient 1,25
Säkerhetsklass 2 = 0,91
Klimatklass 0
Typ så långt kommer jag, kan någon hjälpa mig vidare?
Egentligen vill jag inte att att balken kommer ner mer än kanske ca 250mm från taket då det redan nu endast är 205cm under befintlig balk.
Pelarna tänkte jag typ 3st 45x145 i varje ände.
Bifogar bild på hur jag har det idag till vänster och hur jag skulle vilja ha det till höger.
EDIT: I dagsläget skottar jag taket 1-2ggr per vinter inte för att det behövs men för att det känns bra och hade tänkt fortsätta med det men vill inte heller lämna ett tvång till någon annan om jag skulle gå och dö eller om jag skulle bli sjuk.
Kolla om du hittar en snurra hos svenskt trä.
Alternativt så mäter du nuvarande balk och räknar att du ska ha samma nedböjning i din nya balk som bara har stöd i ändarna. Blir en FET jävla balkajävel men det kostar också att köpa in en beräkningstjänst för detta, tänk ca 10 sillar. Du har en hygglig spännvidd nä du tar bort stöden, trots allt, så snåla inte på det som bär. Stål är inte dumt, det är styvt och kommer ofta i 6 m längder.
Börja typ med en HEA 180. Hittar du en HEB 180 är det ännu bättre. Sen är det bara öka till du får en liten nedböjning.
Obs jag är ej skolad i byggnadskonstruktion, det seriösa är att kontakta en konstruktör.
Även snedsträvor kan vara vettigt, om du kan tillåta det och väggen bär.
Alternativt så mäter du nuvarande balk och räknar att du ska ha samma nedböjning i din nya balk som bara har stöd i ändarna. Blir en FET jävla balkajävel men det kostar också att köpa in en beräkningstjänst för detta, tänk ca 10 sillar. Du har en hygglig spännvidd nä du tar bort stöden, trots allt, så snåla inte på det som bär. Stål är inte dumt, det är styvt och kommer ofta i 6 m längder.
Börja typ med en HEA 180. Hittar du en HEB 180 är det ännu bättre. Sen är det bara öka till du får en liten nedböjning.
Obs jag är ej skolad i byggnadskonstruktion, det seriösa är att kontakta en konstruktör.
Även snedsträvor kan vara vettigt, om du kan tillåta det och väggen bär.
Redigerat:
Man kan göra så att man smäller upp en överdimensionerad stålbalk och hoppas på det bästa. Dock gillar jag inte att jobba på det sättet utan jag vill gärna veta vad det jag har klarar och vad jag har för marginaler.D Den ofrivillige klåparen skrev:
Då är det en konstruktör du ska kontakta.Litenskit skrev:
Ingen kommer göra det jobbet gratis åt dig på nätet. Vill du lära dig själv så är det fackliteratur inom hållfasthetlära och mekanik du behöver, samt studera Eurocode.
Jag är villig att göra det, som du kanske såg i första inlägget så har jag plockat fram en del data. Jag tror dock inte för en sekund att jag måste falla tillbaka ända till grunder med mekanik och hållfasthetslära. Helt övertygad om att det finns tabeller och färdiguträknade värden för vad limträbalkar alternativt stålbalkar klarar för belastning. Detta är inte ett komplext fall med många olika laster att ta hänsyn till. Det är i princip en helt lodrät last som verkar över hela balkens längd.D Den ofrivillige klåparen skrev:
Om jag fattat konstruktionen rätt så gäller följande parametrar:
Balkens längd: 570 cm
Snözon: 3.5
Takåsarnas spännvidd: 580 cm
Egentyngd tak: 0.5 kN/m2
Om vi matar in ovanstående data här:
https://www.byggbeskrivningar.se/dimensionering/pulpettaksbalkar-och-balkar/
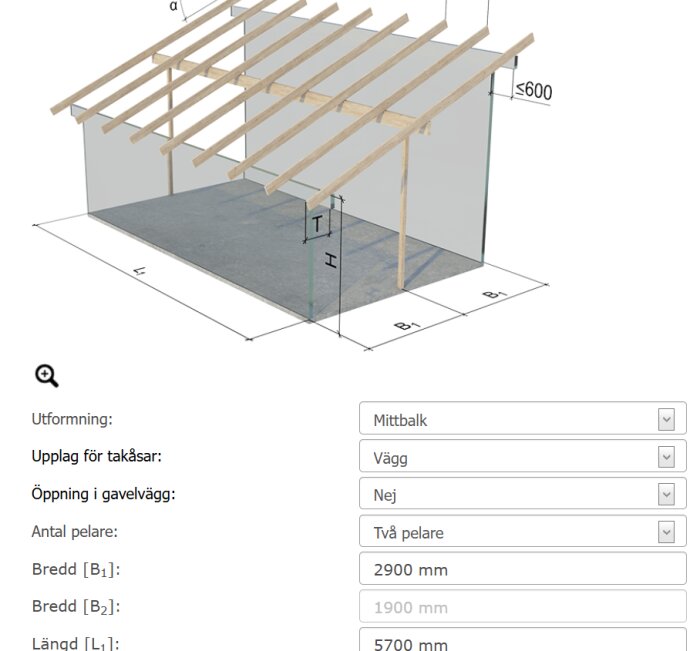
Då spottar deras kalkylator ur sig att kraften i balkens två pelare (i vardera gavel) blir vardera 45,6 kN
Alltså söker vi en balk som kan bära ca 91 kN utbredd last utan att böja ner mer än 1,9cm (Schablonmässigt brukar nedböjning i byggnader begränsas till maximalt: "spännvidd / 300").
Matar vi in denna utbredda last, maximala tillåtna nedböjning och balkens spännvidd i formeln för att beräkna balkböjning för just detta elementarfall (se nedan) så kan vi bryta ut tröghetsmomentet (I) och få följande resultat.
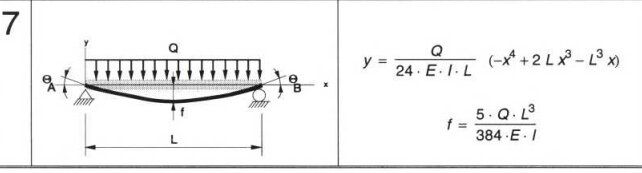
I = 5500 cm4
Slå upp en formelsamling för stålbalkar och välj lämplig profil.
IPE270 har I = 5700 cm4 och klarar därmed jobbet och blir antagligen billigaste lösningen. Men TS ville ha en balk som inte byggde mer än 250mm på höjden.
HEA220 har I = 5410 cm4, det skulle jag våga nöja mig med, om inte välj HEA240 som har god marginal. Båda klarar kravet på önskad bygghöjd.
Balkens längd: 570 cm
Snözon: 3.5
Takåsarnas spännvidd: 580 cm
Egentyngd tak: 0.5 kN/m2
Om vi matar in ovanstående data här:
https://www.byggbeskrivningar.se/dimensionering/pulpettaksbalkar-och-balkar/
Då spottar deras kalkylator ur sig att kraften i balkens två pelare (i vardera gavel) blir vardera 45,6 kN
Alltså söker vi en balk som kan bära ca 91 kN utbredd last utan att böja ner mer än 1,9cm (Schablonmässigt brukar nedböjning i byggnader begränsas till maximalt: "spännvidd / 300").
Matar vi in denna utbredda last, maximala tillåtna nedböjning och balkens spännvidd i formeln för att beräkna balkböjning för just detta elementarfall (se nedan) så kan vi bryta ut tröghetsmomentet (I) och få följande resultat.
I = 5500 cm4
Slå upp en formelsamling för stålbalkar och välj lämplig profil.
IPE270 har I = 5700 cm4 och klarar därmed jobbet och blir antagligen billigaste lösningen. Men TS ville ha en balk som inte byggde mer än 250mm på höjden.
HEA220 har I = 5410 cm4, det skulle jag våga nöja mig med, om inte välj HEA240 som har god marginal. Båda klarar kravet på önskad bygghöjd.
Den verkliga lasten är enligt ovan 4kN/m².
Den dimensionerande lasten är då
5500cm4 är det samma som 55x10^6 mm4?
Om man skulle ta tex 2st HEA220 bredvid varandra skulle man då få dubbla tröghetsmomentet eller räknar man om värdet?
Den dimensionerande lasten är då
Hej, stor tack!G Gabbe1 skrev:
5500cm4 är det samma som 55x10^6 mm4?
Om man skulle ta tex 2st HEA220 bredvid varandra skulle man då få dubbla tröghetsmomentet eller räknar man om värdet?
Enhetsomvandlingen är korrekt.
Två balkar bredvid varandra är två dubbelt så styvt som en balk. Bygger du på höjden är förhållandet exponentiellt (men ställ inte två balkar på varandra, de kan inte ta skjuv emellan dem).
Titta även noga på förhållandet mellan nedböjning och balkens längd: L^3. Dvs ställer du pelarna tex 50 cm in från varje håll har du vunnit mycket.